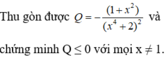Chứng minh : 4x2 -4x +3>0, với mọi giá trị x

Những câu hỏi liên quan
Chứng minh biểu thức sau xác định với mọi giá trị của x:
A
x
2
−
4
x
2
+
1
x
2
+
4...
Đọc tiếp
Chứng minh biểu thức sau xác định với mọi giá trị của x:
A = x 2 − 4 x 2 + 1 x 2 + 4 x + 5 + 3 2 x .
Chứng minh rằng biểu thức:
A = x(x - 6) + 10 luôn luôn dương với mọi x.
B= 4x2
- 4x +3 > 0 với mọi x R
A=\(x^2+6x+9+1\)
=\(\left(x-3\right)^2+1\)
Vì \(\left(x-3\right)^2\)\(\ge\)0 \(\forall\)x
=>\(\left(x-3\right)^2\)+1\(\ge\)1 \(\forall\) x
Vậy A luôn luôn dương với mọi x
B=4\(x^2-4x+1+2\)
=\(\left(2x-1\right)^2+2\)
Vì\(\left(2x-1\right)^2\ge0\forall\) x
=>\(\left(2x-1\right)^2+2\ge2\forall\) x\(\in R\)
Vậy B luôn luôn dương với x thuộc R
Đúng 0
Bình luận (0)
\(A=x\left(x-6\right)+10\)
\(\Leftrightarrow A=x^2-6+10\)
\(\Leftrightarrow A=x^2+4\)
Ta có: \(x^2\ge0\) với mọi x thuộc R
\(\Rightarrow x^2+4\ge4\) với mọi x thuộc R
Do đó A luôn dương với mọi x thuộc R
Đúng 0
Bình luận (4)
a) Với giá trị nào của x thì giá trị biểu thức -1 / 4x + 2 < 0
b) Chứng minh biểu thức -x^2 - 2x - 3 / x^2 + 1 < 0 với mọi x
a)\(\frac{-1}{4x+2}< 0\)
\(\Leftrightarrow4x+2>0\)
\(\Leftrightarrow4x>-2\)
\(\Leftrightarrow x>\frac{-1}{2}\)
Vậy ...
b)\(\frac{-x^2-2x-3}{x^2+1}\)
Ta có: \(-x^2-2x-3=-\left(x+1\right)^2-2\)
Vì \(-\left(x+1\right)^2\le0;\forall x\)
\(\Rightarrow-\left(x+1\right)^2-2\le-2< 0;\forall x\)
Lại có \(x^2\ge0;\forall x\)
\(\Rightarrow x^2+1\ge1>0;\forall x\)
\(\Rightarrow\frac{-x^2-2x-3}{x^2+1}< 0;\forall x\)
Chứng minh giá trị của biểu thức A= 4x^2 - 3x + 1/4x luôn nhận giá trị không âm với mọi x>0
chứng tỏ các bất phương trình sau luôn nghiệm đungs với mọi x
x2 - 4x+5>0
chứng minh rằng -x2+4x-10/x2+1<0 với mọi x
tìm x để biểu thức x2-4x+5 đạt giá trị nhỏ nhất
tìm x để biểu thức -x2+4x+4 đạt giá trị lớn nhất
Ta có :
\(x^2-4x+5=\left(x^2-2.2x+2^2\right)+1=\left(x-2\right)^2+1\ge1>0\)
Vậy đa thức \(x^2-4x+5\) vô nghiệm với mọi giá trị của x
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
chứng minh rằng: -4x2 - 4x - 2 < 0 với mọi giá trị của x
\(-4x^2-4x-2=-\left(4x^2+4x+2\right)=-\left[\left(2x\right)^2+2.2x.1+1+1\right]\)
\(=-\left[\left(2x+1\right)^2+1\right]=-\left(2x+1\right)^2-1\)
Vì \(\left(2x+1\right)^2\ge0\Rightarrow-\left(2x+1\right)^2\le0\Rightarrow-\left(2x+1\right)^2-1\le-1< 0\)
Vậy ta có đpcm.
Đúng 0
Bình luận (0)
chứng minh rằng: -4x2 - 4x - 2 < 0 với mọi giá trị của x
\(-4x^2-4x-2=-\left(4x^2+4x+2\right)=-[\left(2x+1\right)^2+1]\)
Ta có \(\left(2x+1^2\right)\ge0\)\(=>-[\left(2x+1\right)^2+1]\le-1< 0\)
Vậy ...
Học tốt nha !
Đúng 0
Bình luận (0)
Cho phân thức
Q
1
−
x
4
x
10
−
x
8
+
4
x
6
−
4
x
4
+...
Đọc tiếp
Cho phân thức Q = 1 − x 4 x 10 − x 8 + 4 x 6 − 4 x 4 + 4 x 2 − 4 với x ≠ ± 1 .
Chứng minh Q luôn nhận giá trị âm với mọi x ≠ ± 1 .
cho biểu thức A = ( x - 3 ) ( x2 + 3x + 9 ) - ( x - 1 )3 + 4 ( x + 2 ) ( 2 - x ) - x
a. Chứng minh A = - x2 - 4x - 10
b. Chứng minh A luôn có giá trị âm với mọi giá trị của số thực x
a: \(A=x^3-27-x^3+3x^2-3x+1-4\left(x^2-4\right)-x\)
\(=3x^2-4x-26-4x^2+16\)
\(=-x^2-4x-10\)
Đúng 0
Bình luận (0)