Cho hình 39 :
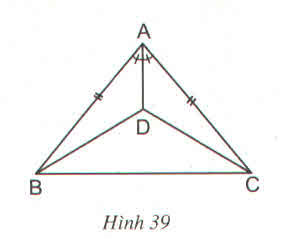
a) Chứng minh \(\Delta ABD=\Delta ACD\)
b) So sánh góc DBC và góc DCB
cho tam giác abc cân tại a điểm d nằm trong tam giác sao cho bad=cad
a, CM rằng tam giác abd = tam giác acd
b,so sánh góc dbc và góc dcb
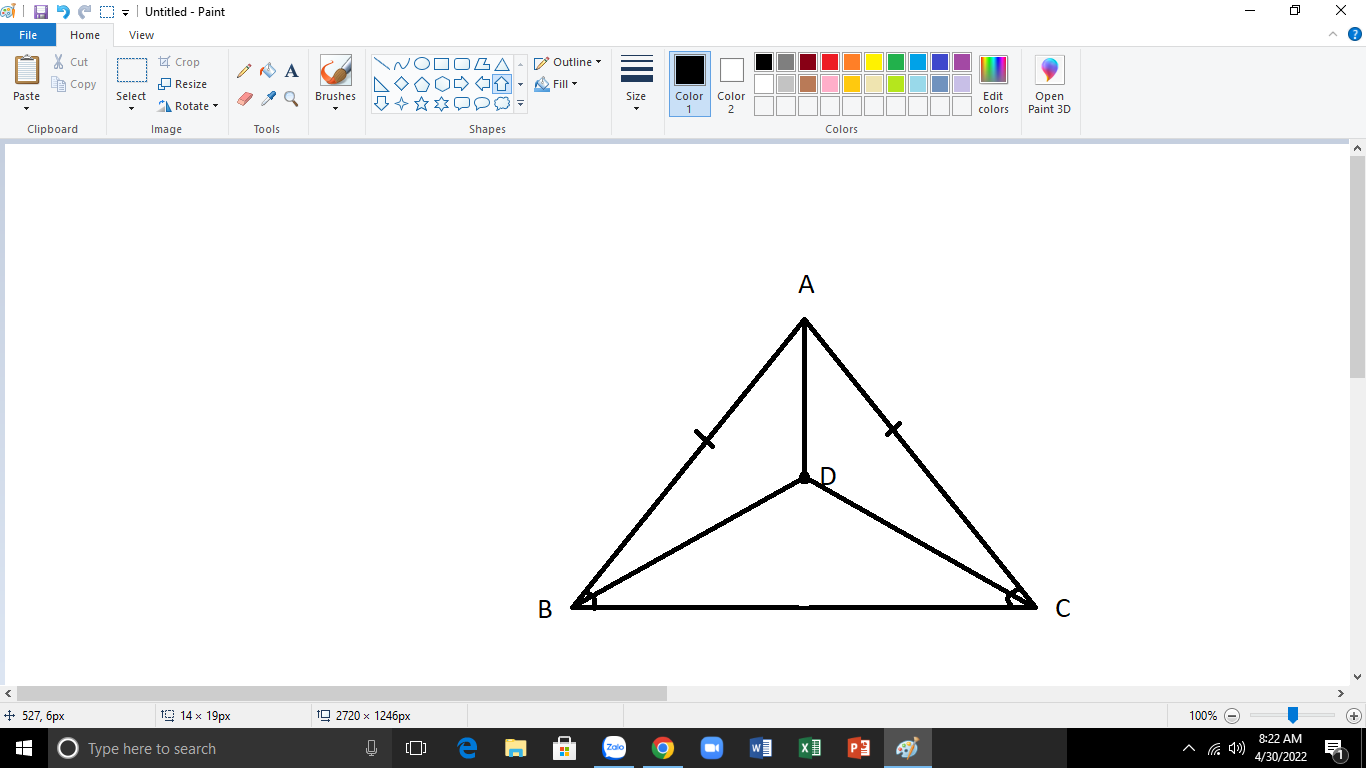
\(\text{a)Xét }\Delta ABD\text{ và }\Delta ACD\text{ có:}\)
\(AB=AC\left(\Delta ABC\text{ cân tại A}\right)\)
\(\widehat{BAD}=\widehat{CAD}\left(gt\right)\)
\(AD\text{ chung}\)
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{ACD}\left(\text{hai góc tương ứng}\right)\)
\(\text{b)Ta có:}\widehat{B}=\widehat{C}\left(\Delta ABC\text{ cân tại A}\right)\)
\(\text{Mà }\widehat{ABD}=\widehat{ACD}\left(cmt\right)\)
\(\Rightarrow\widehat{DBC}=\widehat{DCB}\)
cho tam giác abc cân tại a điểm d nằm trong tam giác sao cho bad=cad
a, CM rằng tam giác abd = tam giác acd
b,so sánh góc dbc và góc dcb
Đây nha:
a. Xét tam giác ABD và tam giác ACD có:
góc BAD = góc BAC (gt)
AD chung
AB = AC (tam giác ABC cân)
=> tam giác ABD = tam giác ACD (cgc)
b. Gọi E là trung điểm của BC
Có: góc BAC = góc BAD + góc CAD mà góc BAD = góc CAD
=> AD là đường phân giác
Lại có: tam giác ABC cân tại A => AD đồng thời là đường trung trực của tam giác ABC
Do đó: DE là đường trung trực cũng là đường phân giác của tam giác BDC.
=> DE vuông với BC tại E; góc BDE = góc CDE
Xét tam giác BDE và tam giác CDE vuông tại E có:
DE chung
góc BDE = góc CDE (cmt)
=> tam giác BDE = tam giác CDE (ch-cgv)
=> góc DBC = góc DCB (2 góc tương ứng)
Cho hình 39.
So sánh góc DBC và góc DCB.
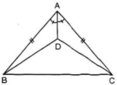
Hình 39
Vì ΔABD = ΔACD (chứng minh câu a)
⇒ BD = CD (hai cạnh tương ứng)
⇒ ΔBCD cân tại D
cho tam giác abc cân tại a. d là điểm nằm trong tam giác sao cho ad là tia phân giác của góc a chứng minh a tam giác abd bằng tam giác acd b góc dbc bằng góc dcb
Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.
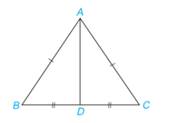
a) Chứng minh rằng \(\Delta \) ABD = \(\Delta \) ACD theo trường hợp cạnh - cạnh - cạnh.
b) Hai góc B và C của tam giác ABC có bằng nhau không?
a) Xét hai tam giác ABD và ACD có:
AB=AC
AD chung
BD=DC
=>\(\Delta \)ABD = \(\Delta \)ACD (c.c.c)
b) Do \(\Delta \)ABD = \(\Delta \)ACD nên \(\widehat B = \widehat C\)( 2 góc tương ứng)
Cho \(\Delta ABC\) có \(AB=AC\). Tia phân giác của góc A cắt BC ở D. Chứng minh:
\(a.\Delta ABD=\Delta ACD\\ b.BD=CD\\ c.AD=BC\)
Ghi cả giả thiết, kết luận nữa ạ
b: ta có: ΔABC cân tại A
mà AD là đường phân giác
nên D là trung điểm của BC
Cho tam giác ABC cân tại A. Điểm D nằm trong tam giác sao cho BAD^ = CAD^ A) chứng minh tam giác ABC = tam giác ACD B) so sánh DBC^ và DCB^
a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó; ΔABD=ΔACD
b: Xét ΔDBC có DB=DC
nên ΔDBC cân tại D
hay \(\widehat{DBC}=\widehat{DCB}\)
Sửa đề chứng minh tam giác ABC = tam giác ACD => △ABD = △ACD
Xét △ABD và △ACD có
AB = AC
AD là cạnh chung
\(\widehat{BAD}=\widehat{CAD}\)
nên △ABD = △ACD (c-g-c)
b)
Ta có:
\(\text{△ABD = △ACD }\)
\(\text{=> DB = DC}\)
\(\text{=> △DBC cân tại D}\)
\(=>\)\(\widehat{DBC}=\widehat{DCB}\)
Cho \(\Delta ABC\) có \(\widehat{B}=\widehat{C}\) . Tia phân giác của góc A cắt BC tại D. Chứng minh: \(\Delta ABD=\Delta ACD\)
Cho tam giác ABC vuông tại A, BD là tia phân giác của góc ABC. Kẻ DE vuông góc với BC tại E, gọi F là giao điểm của BA và ED.
a, Chứng minh \(\Delta ABD=\Delta EBD\)
b, So sánh AD và DC
c, Gọi K là trung điểm của FC. Chứng minh ba điểm B;D;K thẳng hàng.
a, xét 2 t.giác vuông ABD và EBD có:
BD cạnh chung
\(\widehat{ABD}\)=\(\widehat{EBD}\)(gt)
=> t.giác ABD=t.giác EBD(CH-GN)
b,xét 2 t.giác vuông DAF và DEC có:
DA=DE(theo câu a)
\(\widehat{ADF}\)=\(\widehat{EDC}\)(vì đối đỉnh)
=> t.giác DAF=t.giác DEC(cạnh góc vuông-góc nhọn kề)
=> DC=DF(2 cạnh tương ứng) mà DF>DA(vì cạnh huyền lớn hơn cạnh góc vuông)
=> DC>DA đpcm
c,xét \(\Delta\)CBK và \(\Delta\)FBK có:
BK cạnh chung
\(\widehat{FBK}\)=\(\widehat{CBK}\)(gt)
vì AB=EB mà EC=AF nên suy ra FB=CB
=> t.giác CBK=t.giác FBK(c.g.c)
=> \(\widehat{FKB}\)=\(\widehat{CKB}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{FKB}\)=\(\widehat{CKB}\)=90 độ
=> BK\(\perp\)CF
trong t.giác CFB có: FE là đường cao, CA là đường cao
=> BK là đường cao thứ 3 => D là giao điểm của 3 đường cao CA,FE,BK
=> B;D;K thẳng hàng
(câu c mk ko chắc nhé!)