Cho tam giac ABC cân tại A, các đường cao AI, BK, CL cắt nhau tại H.
a)Tìm tâm của đường tròn đi qua 4 điểm A,L,I,C.
b) chứng minh B nằm ngoài đường tròn nói trong câu a.
Cho tam giác ABC cân tại A có các đường cao AH và BK cắt nhau tại I. Chứng minh:
a, Đường tròn đường kính AI đi qua K
b, HK là tiếp tuyến của đường tròn đường kính AI
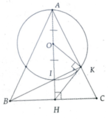
a, Chứng minh được B K A ^ = 90 0
b, Gọi O là trung điểm AI
Ta có:
+ OK = OA => O K A ^ = O A K ^
+ O A K ^ = H B K ^ (cùng phụ A C B ^ )
+ HB = HK => H B K ^ = H K B ^
=> O K A ^ = H K B ^ ⇒ H K O ^ = 90 0
Cho tam giác ABC đều có cạnh = a, các đường cao BD và CE cắt nhau tại H
a) Chứng minh: 4 điểm B,E,D,C thuộc cùng 1 đường tròn. Hãy xác định tâm và bán kính của đường tròn ấy
b) Chứng minh: Điểm H nắm trong đường tròn và điểm A nằm ngoài đường tròn đi qua 4 điểm B,E,D,C
a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp
Tâm là trung điểm của BC
Bán kính là \(\dfrac{BC}{2}=\dfrac{a}{2}\)
Câu 5:(4,0 điểm) Cho tam giác ABC cân (AB = AC). Các đường cao AG, BE, CF gặp nhau tại H.
a. Chứng minh 4 điểm A,E,H,F cùng thuộc một đường tròn. Xác định tâm I của đường tròn ngoại tiếp tứ giác đó.
b. Chứng minh GE là tiếp tuyến của đường tròn tâm I.
c. Chứng minh AH.BE = AF.BC
d. Cho bán kính của đường tròn tâm I là r và góc BAC = α . Hãy tính độ dài đường cao BE của tam giác ABC.
a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^0\)
nên AEHF là tứ giác nội tiếp
c: Xét ΔAFH vuông tại F và ΔCFB vuông tại F có
\(\widehat{FAH}=\widehat{FCB}\)
Do đó: ΔAFH\(\sim\)ΔCFB
Suy ra: AF/CF=AH/CB
hay \(AF\cdot CB=AH\cdot CF\)
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm Ở.các đường cao AD,BE cắt nhau tại H.Gọi I là tâm đường tròn đi qua 3 điểm A,E,H.a) xác định vị trí tương đối của (I) và (O) ;b) AB cắt (I) tại F.c/m : C,H,F thẳng hàng
cho tam giác ABC cân tại A có các đường cao AD,BE,CF cắt nhau tại H
a) CM 4 diem D,B,H,F cung thuoc 1 đường tròn xác định tâm I của đường tròn này
b) CM 4 điểm A.,F,D,C cùng thuộc 1 đường tròn xác định tâm K của đường tròn này
c) I di qua trung điểm của FD
d) B nằm ngoài đường tròn K đã nêu ở câu b
tam giác ABC đều các đường cao BD và CE cắt nhau tại H
chứng minh 4 điểm B E D C cùng thuộc 1 đường tròn. XÁc định tâm và bán kính của đường tròn ấy.
chứng minh điểm hH nằm trong đg tròn và điểm A nằm ngoài đg tròn và đi qua 4 điểm B E D C
- có \(\Delta BDC\)vuông tại D
nên D thuộc đường tròn đường kính BC ( 1)
có \(\Delta BEC\)vuông tại E
nên E thuộc đường tròn đường kính BC (2)
từ (1) và (2) suy ra đpcm
- gọi O là trung điểm của BC
có AO vuông góc với BC
dễ thấy OE > OH
nên H nằm trong đường tròn đường kính BC
dễ cm OA > OB
ên A nằm ngoài đường tròn đường kính BC
cho tam giác ABC cân tại A (A<90), hai đường cao BD và CE cắt nhau tại H.
a. Chứng minh bốn điểm A,D,H,E cùng thuộc đường tròn, xác định tâm Ovaf vẽ đường tròn này.
b. Gọi K là giao điểm cảu AO và BC, Chứng minh KD là tiếp tuyến của đường tròn (O)
a: góc ADH+góc AEH=180 độ
=>ADHE nội tiếp
O là trung điểm của AH
b:
XetΔACB có
BD,CE là đường cao
BD căt CE tại H
=>H là trực tâm
=>AH vuông góc BC
=>K là trung điểm của CB
góc ODK=góc ODH+góc KDH
=góc BHK+góc KBH=90 độ
=>KD là tiếp tuyến của (O)
Cho tam giác ABC đều có cạnh là a các đường cao BD và CE cắt nhau tại H
a)Chứng minh rằng B , E , D ,C cùng thuộc đường tròn
b)Hãy xác định tâm và bán kính của đường tròn đó
c) Chứng minh rằng điểm H nằm trong đường tròn và điểm A nằm ngoài đường tròn biết a = 2 cm
d )Tính OH
a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp
=>B,E,D,C cùng thuộc 1 đường tròn
b: Vì \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên B,E,D,C cùng thuộc đường tròn đường kính BC
tâm là trung điểm I của BC
bán kính là BC/2
c: Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC(1)
ΔABC cân tại A
mà AI là đường trung tuyến
nên AI\(\perp\)BC(2)
Từ (1),(2) suy ra A,H,I thẳng hàng
ΔABC đều
mà BD,CE là các đường cao
nên BD,CE là các đường trung tuyến
=>D,E lần lượt là trung điểm của AC,AB
Xét ΔABC có
BD,CE là các đường trung tuyến
BD cắt CE tại H
Do đó; H là trọng tâm của ΔABC
mà I là trung điểm của BC
nên \(AH=\dfrac{2}{3}AI\) và \(IH=\dfrac{1}{3}IA\)
ΔAIB vuông tại I
=>\(AB^2=AI^2+IB^2\)
=>\(AI^2=2^2-1^2=3\)
=>\(AI=\sqrt{3}\left(cm\right)\)
\(HI=\dfrac{1}{3}HA=\dfrac{1}{3}\sqrt{3}< \dfrac{1}{3}\cdot3=IB=R\)
=>H nằm trong (I)
\(IA=\sqrt{3}>1=IB=R\)
=>A nằm ngoài (I)
Cho tam giác ABC cân Tại A đường cao AH và BK cắt nhau tại I
a) Chứng minh tam giác BKH cân tại H
b) Gọi O là trung điểm của AI .Chứng Minh góc BKH = góc IAK
c) Chứng minh HK là tiếp tuyến của đường tròn tâm O
a: Ta có: ΔBKC vuông tại K
mà KH là trung tuyến
nên KH=BH
=>ΔHBK cân tại H
b: góc BAH=90 độ-góc ABC
góc IAK=90 độ-góc ACB
mà góc ABC=góc ACB
nên góc BAH=góc IAK
c: Gọi G là trung điểm của AI
góc GKH=góc GKI+góc HKI
=góc GIK+góc HBI
=góc BIH+góc HBI=90 độ
=>HK là tiếp tuyến của (G)