Cho ba điểm \(A\left(3;5\right);B\left(2;3\right);C\left(6;2\right)\)
a) Viết phương trình đường tròn (C) ngoại tiếp tam giác ABC
b) Hãy xác định tọa độ của tâm và bán kính của (C)
Câu 3. Trong mặt phẳng tọa độ $Oxy$ cho ba điểm $A\left( 4;6 \right), \, B\left( -3;5 \right), \, C\left( 1;7 \right)$.
a) Viết phương trình đường tròn $\left( T \right)$ đi qua ba điểm $A, \, B, \, C$. Tìm tọa độ tâm $I$ và tính bán kính của đường tròn $\left( T \right)$.
b) Viết phương trình các tiếp tuyến của đường tròn biết tiếp tuyến song song với trục tọa độ.
a: Đặt I(x;y)
I(x;y); A(4;6); B(-3;5); C(1;7)
\(IA^2=\left(4-x\right)^2+\left(6-y\right)^2=\left(x-4\right)^2+\left(y-6\right)^2\)
\(IB^2=\left(-3-x\right)^2+\left(5-y\right)^2=\left(x+3\right)^2+\left(y-5\right)^2\)
\(IC^2=\left(1-x\right)^2+\left(7-y\right)^2=\left(x-1\right)^2+\left(y-7\right)^2\)
I là tâm đường tròn ngoại tiếp ΔABC nên IA=IB=IC
=>\(IA^2=IB^2=IC^2\)
=>\(\begin{cases}\left(x-4\right)^2+\left(y-6\right)^2=\left(x+3\right)^2+\left(y-5\right)^2\\ \left(x+3\right)^2+\left(y-5\right)^2=\left(x-1\right)^2+\left(y-7\right)^2\end{cases}\)
=>\(\begin{cases}x^2-8x+16+y^2-12y+36=x^2+6x+9+y^2-10y+25\\ x^2+6x+9+y^2-10y+25=x^2-2x+1+y^2-14y+49\end{cases}\)
=>\(\begin{cases}-8x-12y+52=6x-10y+34\\ 6x-10y+34=-2x-14y+50\end{cases}\)
=>\(\begin{cases}-14x-2y=-18\\ 8x+4y=16\end{cases}\Rightarrow\begin{cases}-28x-4y=-36\\ 8x+4y=16\end{cases}\)
=>\(\begin{cases}-28x-4y+8x+4y=-36+16\\ 8x+4y=16\end{cases}\Rightarrow\begin{cases}-20x=-20\\ 2x+y=4\end{cases}\)
=>\(\begin{cases}x=1\\ y=4-2x=4-2=2\end{cases}\)
=>I(1;2)
I(1;2); A(4;6)
\(IA^2=\left(4-1\right)^2+\left(6-2\right)^2=3^2+4^2=25\)
=>\(R=\sqrt{25}=5\)
Phương trình đường tròn (T) là:
\(\left(x-1\right)^2+\left(y-2\right)^2=R^2=25\)
Cho ba điểm A, B, C. Chứng minh \(3\left( {\overrightarrow {AB} + 2\overrightarrow {BC} } \right) - 2\left( {\overrightarrow {AB} + 3\overrightarrow {BC} } \right) = \overrightarrow {AB} \)
Ta có: \(3\left( {\overrightarrow {AB} + 2\overrightarrow {BC} } \right) - 2\left( {\overrightarrow {AB} + 3\overrightarrow {BC} } \right)\)\( = 3\overrightarrow {AB} + 3.\left( {2\overrightarrow {BC} } \right) - \left[ {2\overrightarrow {AB} + 2.\left( {3\overrightarrow {BC} } \right)} \right]\)
\[ = 3\overrightarrow {AB} + 6.\overrightarrow {BC} - \left( {2\overrightarrow {AB} + 6.\overrightarrow {BC} } \right)\]\[ = 3\overrightarrow {AB} + 6.\overrightarrow {BC} - 2\overrightarrow {AB} - 6.\overrightarrow {BC} \]
\[ = \left( {3\overrightarrow {AB} - 2\overrightarrow {AB} } \right) + \left( {6.\overrightarrow {BC} - 6.\overrightarrow {BC} } \right) = \overrightarrow {AB} .\]
Cho hai bộ ba điểm :
a) \(A=\left(1;3;1\right);B=\left(0;1;2\right);C=\left(0;0;1\right)\)
b) \(M=\left(1;1;1\right);N=\left(-4;3;1\right):P=\left(-9;5;1\right)\)
Hỏi bộ nào có 3 điểm thẳng hàng ?
a) Cho \(A\left(-1;8\right);B\left(1;6\right);C\left(3;4\right)\). Chứng minh ba điểm A, B, C thẳng hàng ?
b) Cho \(A\left(1;1\right);B\left(3;2\right)\) và \(C\left(m+4;2m+1\right)\). Tìm m để 3 điểm A. B. C thẳng hàng ?
a) \(\overrightarrow{AB}\left(2;-2\right)\); \(\overrightarrow{CA}=\left(4;-4\right)\).
Vì \(\dfrac{2}{4}=\dfrac{-2}{-4}\) nên \(\overrightarrow{AB};\overrightarrow{CA}\) cùng phương . Suy ra ba điểm A, B, C thẳng hàng.
\(\overrightarrow{AB}\left(2;1\right)\); \(\overrightarrow{AC}\left(m+3;2m\right)\).
3 điểm A, B, C thẳng hàng nên hai véc tơ \(\overrightarrow{AB},\overrightarrow{AC}\) cùng phương.
Suy ra: \(\dfrac{m+3}{2}=\dfrac{2m}{1}\Leftrightarrow m+3=4m\)\(\Leftrightarrow m=1\).
Cho ba điểm \(B=\left(-2;3\right)\) ;\(C=\left(3;3\right)\) ;\(D=\left(3;-2\right)\) . Biết A là điểm có tọa độ sao cho 4 điểm A; B; C; D tạo thành hình vuông. Tính diện tích hình vuông ABCD.
Theo hệ trục toạ độ ( bạn tự vẽ nha ), để ABCD là hình vuông => \(A\left(-2;-2\right)\)
Ta có : độ dài AB=\(\sqrt{\left(-2+2\right)^2+\left(-2-3\right)^2}=\sqrt{25}=5\)
=> Diện tích của hình v ABCD=\(5^2=25\)( đơn vị )
Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\)
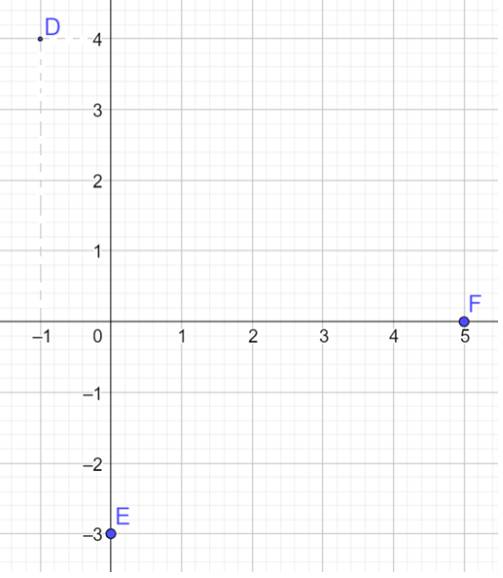
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy
b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \).
c) Vẽ và tìm tọa độ hai vectơ đơn vị và \(\overrightarrow j \)lần lượt trên hai trục tọa độ Ox và Oy
a)
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
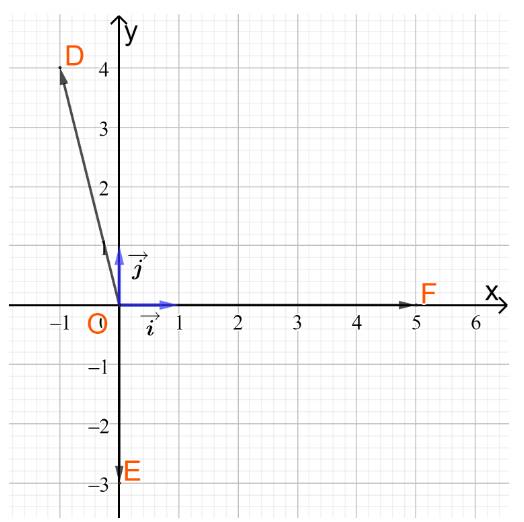
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)
Trong mặt phẳng Oxy cho 3 điểm \(A\left(-1;-1\right);B\left(3;1\right);C\left(6;0\right)\) ?
a) Chứng minh ba điểm A, B, C không thẳng hàng
b) Tính góc B của tam giác ABC
a) \(\overrightarrow{BA}\left(4;2\right);\overrightarrow{BC}\left(3;-1\right)\).
Vì \(\dfrac{4}{3}\ne\dfrac{2}{-1}\) nên hai véc tơ \(\overrightarrow{BA};\overrightarrow{BC}\) không cùng phương hay 3 điểm A, B, C không thẳng hàng.
b) \(cos\widehat{ABC}=cos\left(\overrightarrow{BA};\overrightarrow{BC}\right)=\dfrac{4.3+2.\left(-1\right)}{\sqrt{4^2+2^2}.\sqrt{3^2+\left(-1\right)^2}}\)\(=\dfrac{\sqrt{2}}{2}\).
Suy ra: \(\widehat{ABC}=45^o\).
1. Trong mặt phẳng tọa độ xOy cho ba điểm \(A\left(5,-8\right),B\left(-3,-2\right),C\left(11,0\right)\). Xác định tọa độ điểm M thuộc Ox sao cho\(\overrightarrow{AM}.\overrightarrow{MB}\) có giá trị nhỏ nhất.
2. Cho tam giác ABC có góc nhọn A, D và E lần lượt là hai điểm nằm ngoài tam giác sao cho tam giác ABD và tam giác ACE vuông cân tại A. M là trung điểm của BC. Chứng minh \(AM\perp DE\)
3. Trong mặt phẳng tọa độ xOy cho ba điểm \(A\left(1,2\right),B\left(-3,0\right),C\left(0,4\right)\). Xác định tọa độ điểm M thuộc Ox sao cho\(\left|\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}\right|\) có giá trị nhỏ nhất.
Cho tam giác ABC
a) Tìm điểm N sao cho \(2\overrightarrow{NA}+\overrightarrow{NB}=3\overrightarrow{BC}\)
b) Tìm tập hợp các điểm M sao cho \(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{BA}-\overrightarrow{BC}\right|\)
a) Từ điểm I trên AB thỏa mãn IA = 1/2 IB ta vẽ đường song song với BC. Điểm N nằm trên đó.
B) tương tự câu a)
Trong hệ trục tọa độ Oxy cho ba điểm A(1; -4) , B(4;5) và C(0;-9). Điểm M di chuyển trên trục Ox . Đặt Q=\(2\left|\overrightarrow{MA}+2\overrightarrow{MB}\right|+3\left|\overrightarrow{MB}+\overrightarrow{MC}\right|\) . Biết giá trị nhỏ nhất của Q có dạng \(a\sqrt{b}\)
trong đó a, b là các số nguyên dương a, c< 20. Tính a-b
Do M thuộc Ox, gọi tọa độ M có dạng \(M\left(m;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-m;-4\right)\\\overrightarrow{MB}=\left(4-m;5\right)\\\overrightarrow{MC}=\left(-m;-9\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+2\overrightarrow{MB}=\left(9-3m;6\right)\\\overrightarrow{MB}+\overrightarrow{MC}=\left(4-2m;-4\right)\end{matrix}\right.\)
\(Q=2\sqrt{\left(9-3m\right)^2+6^2}+3\sqrt{\left(4-2m\right)^2+\left(-4\right)^2}\)
\(=\sqrt{\left(6m-18\right)^2+12^2}+\sqrt{\left(12-6m\right)^2+12^2}\)
\(=\sqrt{\left(18-6m\right)^2+12^2}+\sqrt{\left(6m-12\right)^2+12^2}\)
\(Q\ge\sqrt{\left(18-6m+6m-12\right)^2+\left(12+12\right)^2}=6\sqrt{17}\)
\(\Rightarrow a-b=-11\)