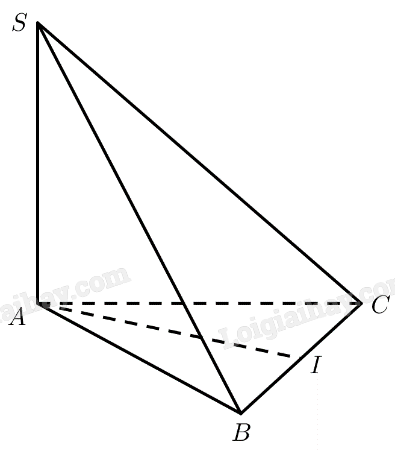
Gọi \(I\) là trung điểm của \(BC\).

Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)

\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AI\)

\( \Rightarrow d\left( {SA,BC} \right) = AI = \frac{{BC\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)

Mk cho mk nhé

Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.

Ta có cái này: \(\vec{HG}=\dfrac{2}{3}\vec{HO}\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{3}-3=\dfrac{2}{3}\left(x_O-3\right)\\\dfrac{8}{3}-2=\dfrac{2}{3}\left(y_O-2\right)\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_O=1\\y_O=3\end{matrix}\right.\Rightarrow O=\left(1;3\right)\)

\(d\left(O;BC\right)=\dfrac{\left|1+2.3-2\right|}{\sqrt{5}}=\sqrt{5}\)

Phương trình trung trực BC: \(2x-y+1=0\)

\(\Rightarrow\) Trung điểm M của BC có tọa độ là nghiệm hệ:

\(\left\{{}\begin{matrix}2x-y+1=0\\x+2y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\Rightarrow M=\left(0;1\right)\)

Lại có \(\vec{AG}=\dfrac{2}{3}\vec{AM}\Rightarrow A=\left(5;6\right)\)

\(\Rightarrow R=OA=5\)

Phương trình đường tròn ngoại tiếp:

\(\left(x-1\right)^2+\left(y-3\right)^2=25\)

Giống mình làm

Bằng nhau

a=b=c=1 suy ra Tam giác ABC là tam giác đều vì có độ dài 3 canh = nhau .

ta áp dụng (a+b+c)(\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)) >=9 

dễ chứng minh bdt phụ này 

rùi từ đây suy ra 3(a-b)(b-c)(c-a) = 0 => a=b=c (1)

mà lên bđt phụ trên thì xảy ra khi a=b=c (1)

từ (1) , (2) , ta suy ra a=b=c hay đpcm 

vì k chặt chẽ lắm nên thông cảm

Đây là nâng cao à,khó quá mk học lớp 8 nhưng ko giải đc

nick mi đổi tên ah

https://olm.vn/hoi-dap/detail/80860541793.html

Ta có : \(\overrightarrow{AB}=\left(-a;b;0\right)\)

và \(\overrightarrow{AC}=\left(-a;0;c\right)\)

Vì \(\overrightarrow{AB}.\overrightarrow{AC}=a^2>0\) nên góc \(\widehat{BAC}\) là góc nhọn

Lập luận tương tự chứng minh được các góc \(\widehat{B}\) và \(\widehat{C}\) cũng là góc nhọn

a) \(\cos A=-\dfrac{3}{5}\Rightarrow\widehat{A}\approx126^052'\)

b) \(AB:2x+y-1=0;AC=2x-y-3=0\)

c) Phân giác trong \(AD\) có phương trình : \(y+1=0\)

a) \(x_G=\dfrac{-3+9+\left(-5\right)}{3}=\dfrac{1}{3}\).
\(y_G=\dfrac{6+\left(-10\right)+4}{3}=0\).
Vậy \(G\left(\dfrac{1}{3};0\right)\).
b) Tứ giác BGCD là hình bình hành khi và chỉ khi:
\(\overrightarrow{BG}=\overrightarrow{CD}\).
Gọi \(D\left(x;y\right)\).
\(\overrightarrow{BG}\left(-\dfrac{26}{3};10\right);\overrightarrow{CD}\left(x+5;y-4\right)\).
Do \(\overrightarrow{BG}=\overrightarrow{CD}\) nên \(\left\{{}\begin{matrix}x+5=-\dfrac{26}{3}\\y-4=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{41}{3}\\y=14\end{matrix}\right.\).
Vậy \(D\left(-\dfrac{41}{3};14\right)\).