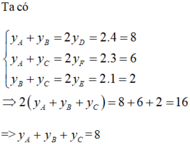trong mặt phẳng Oxy cho tam giác ABC có trung điểm cạnh BC là M (3;2) trọng tâm G và tâm đường tròn ngoại tiếp tam giác ABC lần lượt là G(2/3; 2/3) ; I (1;-2) tìm tọa độ đỉnh C

Những câu hỏi liên quan
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G 2 3 ; 0 , biết M(1;1) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A.(2;0)
B.(-2;0)
C.(0;-2)
D.(0;2)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm
G
(
2
3
;
0
)
, biết
M
(
1
;
1
)
là trung điểm cạnh BC. Tọa độ đỉnh A là: A. (2;0) B. (-2;0) C. (0;-2) D. (0;2)
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G ( 2 3 ; 0 ) , biết M ( 1 ; 1 ) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A. (2;0)
B. (-2;0)
C. (0;-2)
D. (0;2)
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
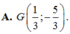
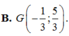
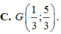
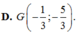
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trung điểm các cạnh BC, CA, AB tương ứng là M(2 ; 0), N4 ; 2), P(1 ; 3).
a) Tìm toạ độ các điểm A, B, C.
b) Trọng tâm hai tam giác ABC và MNP có trùng nhau không? Vì sao?
a) Do M, N, P là trung điểm của các cạnh BC, CA, AB nên:
\(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = {x_M}\\\frac{{{x_B} + {x_A}}}{2} = {x_P}\\\frac{{{x_A} + {x_C}}}{2} = {x_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = 4\\{x_B} + {x_A} = 2\\{x_A} + {x_C} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 3\\{x_B} = - 1\\{x_C} = 5\end{array} \right.\) và \(\left\{ \begin{array}{l}\frac{{{y_B} + {y_C}}}{2} = {y_M}\\\frac{{{y_B} + {y_A}}}{2} = {y_P}\\\frac{{{y_A} + {y_C}}}{2} = {y_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_B} + {y_C} = 0\\{y_B} + {y_A} = 4\\{y_A} + {y_C} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_A} = 5\\{y_B} = - 1\\{y_C} = 1\end{array} \right.\)
Vậy \(A\left( {3;5} \right),B\left( { - 1; - 1} \right),C\left( {5;1} \right)\)
b) Trọng tâm tam giác ABC có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{3 + \left( { - 1} \right) + 5}}{3} = \frac{7}{3}\\\frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{5 + \left( { - 1} \right) + 1}}{3} = \frac{5}{3}\end{array} \right.\)
Trọng tâm tam giác MNP có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 4 + 1}}{3} = \frac{7}{3}\\\frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{0 + 2 + 3}}{3} = \frac{5}{3}\end{array} \right.\)
Vậy trọng tâm của 2 tam giác ABC và MNP là trùng nhau vì có cùng tọa độ.
Đúng 1
Bình luận (0)
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;-4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC. A.
G
1
3
;
-
5
3
B.
G
-
1
3
;...
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;-4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
A. G 1 3 ; - 5 3
B. G - 1 3 ; 5 3
C. G 1 3 ; 5 3
D. G - 1 3 ; - 5 3
Trong mặt phẳng của hệ tọa độ Oxy , cho tam giác ABC có AB AC , widehat{BAC} 90 độ . Biết M(1 ; -1 ) là trung điểm của cạnh BC và G ( dfrac{2}{3} ; 0 ) là trọng tâm tam giác ABC . Khi đó , A ( xa ; yb ) , B ( xa ; yb ) (xb 0 ) . Tính 2019 x2A + y A + 2xB - 3yB.
Đọc tiếp
Trong mặt phẳng của hệ tọa độ Oxy , cho tam giác ABC có AB = AC , \(\widehat{BAC}\) = 90 độ . Biết M(1 ; -1 ) là trung điểm của cạnh BC và G ( \(\dfrac{2}{3}\) ; 0 ) là trọng tâm tam giác ABC . Khi đó , A ( xa ; yb ) , B ( xa ; yb ) (xb < 0 ) . Tính 2019 x2A + y A + 2xB - 3yB.
Trong mặt phẳng tọa độ Oxy cho tam giác ABC có D(3;4), E (6;1), F (7;3) lần lượt là trung điểm các cạnh AB, BC,CA. Tính tổng tung độ của ba đỉnh tam giác ABC. A.
16
3
B.
8
3
C. 8 D. 16
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho tam giác ABC có D(3;4), E (6;1), F (7;3) lần lượt là trung điểm các cạnh AB, BC,CA. Tính tổng tung độ của ba đỉnh tam giác ABC.
A. 16 3
B. 8 3
C. 8
D. 16
Trong mặt phẳng tọa độ oxy cho hình bình hành ABCD có A(0,8). Trung điểm các cạnh DC, BC lần lượt là M(4;-1) và N(2;5). Tìm G là trọng tâm tam giác ABC?
Trong mặt phẳng Oxy , cho tam giác ABC có đường tròn nội tiếp tiếp xúc với 3 cạnh BC,CA,AB lần lượt tại M,N,P .Gọi D là trung điểm cạnh BC .Biết M(-1,1) , pt NP: x+y-4=0 và pt AD: 14x--13y+7=0 .Tìm tọa độ điểm A
Trong mặt phẳng tọa đọ Oxy, cho tam giác ABC vuông tại A có AC=2AB. Diểm M là trung điểm của cạnh BC. E thuộc AC/ AE=3EC. chứng minh AM vuông với BE