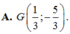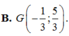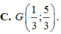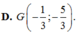Các câu hỏi tương tự
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M(4;-1),N(0;-5) lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x- 3y+5 0, trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC.
Đọc tiếp
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M(4;-1),N(0;-5) lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x- 3y+5 = 0, trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC.
![]()
![]()
![]()
![]()
Cho
∆
A
B
C
có trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM? A.
V
A
;
-
1
2
B.
V
G...
Đọc tiếp
Cho ∆ A B C có trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM?
A. V A ; - 1 2
B. V G ; 1 2
C. V G ; - 2
D. V G ; - 1 2
Câu 4: (0.5 điểm) ) Cho hình chóp S.ABC , gọi M, N lần lượt là trung điểm của các cạnh SA, SC. Biết G là trọng tâm của tam giác ABC. Tìm giao điểm của đường thẳng SG và mặt phẳng (BMN)
Cho tứ diện ABCD. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, BD,CD.
a. Xác định giao tuyến của hai mặt phẳng (AMN) và (ACD).
b. Chứng minh rằng đường thẳng BC song song với mặt phẳng (ANP)
c. Gọi G, H lần lượt là trọng tâm của tam giác ABC và ACD. Chứng minh GH // BD.
Cho tam giác ABC với trọng tâm G. Gọi A,B,C lần lượt là trung điểm của các cạnh BC,AC,AB của tam giác ABC. Phép vị tự biến tam giác ABC thành tam giác ABC là A. Phép vị tự tâm G, tỉ số k2 B. Phép vị tự tâm G, tỉ số k-2 C. Phép vị tự tâm G, tỉ số k-3 D. Phép vị tự tâm G, tỉ số k3
Đọc tiếp
Cho tam giác ABC với trọng tâm G. Gọi A',B',C' lần lượt là trung điểm của các cạnh BC,AC,AB của tam giác ABC. Phép vị tự biến tam giác A'B'C' thành tam giác ABC là
A. Phép vị tự tâm G, tỉ số k=2
B. Phép vị tự tâm G, tỉ số k=-2
C. Phép vị tự tâm G, tỉ số k=-3
D. Phép vị tự tâm G, tỉ số k=3
Cho tam giác ABC có trọng tâm G, Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Mệnh đề nào sau đây là sai. A.
T
1
/
2
B
C
→
(
F
)
E
B .
T...
Đọc tiếp
Cho tam giác ABC có trọng tâm G, Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Mệnh đề nào sau đây là sai.
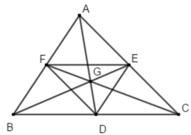
A. T 1 / 2 B C → ( F ) = E
B . T D E → ( B ) = F
C. T 2 D G → ( A ) = G
D. T 1 / 2 G A → ( D ) = G
Cho tam giác ABC với trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm các cạnh BC, AC, AB của tam giác ABC. Khi đó, phép vị tự nào biến tam giác A’B’C’ thành tam giác ABC? A. Phép vị tự tâm G, tỉ số 2 B. Phép vị tự tâm G, tỉ số –2 C. Phép vị tự tâm G, tỉ số
−
2
3
D. Phép vị tự tâm G, tỉ số
−
1
2
Đọc tiếp
Cho tam giác ABC với trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm các cạnh BC, AC, AB của tam giác ABC. Khi đó, phép vị tự nào biến tam giác A’B’C’ thành tam giác ABC?
A. Phép vị tự tâm G, tỉ số 2
B. Phép vị tự tâm G, tỉ số –2
C. Phép vị tự tâm G, tỉ số − 2 3
D. Phép vị tự tâm G, tỉ số − 1 2
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.
Phép vị tự tâm G tỉ số -1/2 biến tam giác ABC thành
A. Tam giác GBC
B. Tam giác DEF
C. Tam giác AEF
D. Tam giác AFE
Cho hình lăng trụ tam giác ABC A'B'C'. Gọi K M N E lần lượt là trung điểm của các cạnh CC' AB AA' và BB' . G là trọng tâm tam giác ABC, I là điểm thuộc đoạn BC sao cho BI = 1/3 BC. CMR
a/ (MNC) // (A'BK)
b/ (MNK) // (A'BC')
c/ ( GKN) // (A'IC')
Giúp mình câu c với ạ