(c) x2 + y2 + 2x -4y -5=0 và điểm M(1;-4)
Chứng tỏ M nằm trong đưởng tròn (c) và cắt (c) tại 2 điểm A và B sao cho AB ngắn nhất
Những câu hỏi liên quan
Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng.
a) x2 + y2 + xy + 4x – 2 = 0;
b) x2 + y2 – 2x – 4y + 5 = 0;
c) x2 + y2 + 6x – 8y + 1 = 0.
a) Đây không phải là phương trình đường tròn do có \(xy\).
b) Vì \({a^2} + {b^2} - c = {1^2} + {2^2} - 5 = 0\)nên phương trình đã cho không là phương trình tròn.
c) Vì \({a^2} + {b^2} - c = {\left( { - 3} \right)^2} + {4^2} - 1 = 24 > 0\)nên phương trình đã cho là phương trình tròn có tâm \(I\left( { - 3;4} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} = 2\sqrt 6 \).
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 0 và đường tròn (C) có phương trình
x
2
+
y
2
−
2
x
+
4
y
–
4
0
. Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 = 0 và đường tròn (C) có phương trình x 2 + y 2 − 2 x + 4 y – 4 = 0 . Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox .
Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
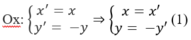
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0.
Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x ' 2 + y ' 2 − 2 x ′ + 4 y ′ − 4 = 0 .
Từ đó suy ra phương trình của (C') là x − 1 2 + y − 2 2 = 9 .
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3,
từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là x − 1 2 + y − 2 2 = 9
Đúng 0
Bình luận (0)
Cho đường tròn (C) có phương trình
x
2
+
y
2
-
2
x
+
4
y
+
4
0
và điểm A(5; -5). Góc α của các tiếp tuyến với đường tròn (C) kẻ từ A thỏa mãn A.
sin
α
2
1
5
B.
sin
α
1
5...
Đọc tiếp
Cho đường tròn (C) có phương trình x 2 + y 2 - 2 x + 4 y + 4 = 0 và điểm A(5; -5). Góc α của các tiếp tuyến với đường tròn (C) kẻ từ A thỏa mãn
A. sin α 2 = 1 5
B. sin α = 1 5
C. cos α 2 = 1 5
D. cos α = 2 5
Có bao nhiêu số thực m để tôn tại duy nhất cặp số thực (x;y) thỏa mãn đồng thời
log
x
2
+
y
2
+
2
4
x
+
4
y
+
m
2
-...
Đọc tiếp
Có bao nhiêu số thực m để tôn tại duy nhất cặp số thực (x;y) thỏa mãn đồng thời log x 2 + y 2 + 2 4 x + 4 y + m 2 - m - 5 ≥ 1 và x 2 + y 2 + 2 x - 4 x + 1 = 0 .
A. 2.
B. 6.
C. 4.
D. 0.
Tìm tọa độ giao điểm của đường thẳng d: x- 2y + 3 0 và đường tròn (C): x2+ y2- 2x – 4y 0 A. (3; 3) và (-1; 1) B. (1;1) và (-3;3) C. (3; -3) D. Đáp án khác
Đọc tiếp
Tìm tọa độ giao điểm của đường thẳng d: x- 2y + 3= 0 và đường tròn (C): x2+ y2- 2x – 4y = 0
A. (3; 3) và (-1; 1)
B. (1;1) và (-3;3)
C. (3; -3)
D. Đáp án khác
Tọa độ giao điểm của đường thẳng và đường tròn là nghiệm của hệ phương trình sau
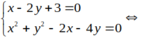
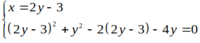
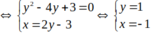hoặc 
Vậy tọa độ giao điểm là (3;3) và (-1; 1) .
Chọn A.
Đúng 0
Bình luận (0)
Cho hai đường tròn
C
1
:
x
2
+
y
2
−
6
x
−
4
y
+
9
0
v
à
C
2
:
x
2
+
y
2
−
2
x
−
8
y
+...
Đọc tiếp
Cho hai đường tròn C 1 : x 2 + y 2 − 6 x − 4 y + 9 = 0 v à C 2 : x 2 + y 2 − 2 x − 8 y + 13 = 0 . Giao điểm của hai đường tròn là
A.A(1; 3), B(2; 4)
B.A(1; 2), B(3; 4)
C.A(1; 4), B(2; 3)
D. Không tồn tại
Tọa độ giao điểm là nghiệm của hệ phương trình
x 2 + y 2 − 6 x − 4 y + 9 = 0 x 2 + y 2 − 2 x − 8 y + 13 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 − 4 x + 4 y − 4 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 ( 1 ) x − y + 1 = 0 ( 2 )
Từ (2) suy ra: y = x+ 1 thay vào (1) ta được:
x 2 + ( x + 1 ) 2 - 6 x – 4 ( x + 1 ) + 9 = 0 x 2 + x 2 + 2 x + 1 - 6 x - 4 x – 4 + 9 = 0
2 x 2 – 8 x + 6 = 0
Vậy 2 đường tròn đã cho cắt nhau tại 2 điểm là (1; 2) và (3;4).
ĐÁP ÁN B
Đúng 0
Bình luận (0)
Các giao điểm của đường thẳng ∆: x – y + 4 0 và đường tròn (C) có phương trình
x
2
+
y
2
+
2
x
−
4
y
−
8
0
là A.M(-4;0) và M(3; 7) B.M(1;5) và M(-2; 2) C.M(0; 4) và M(-3; 1) D.M(1; 5) và M(- 4; 0)
Đọc tiếp
Các giao điểm của đường thẳng ∆: x – y + 4 = 0 và đường tròn (C) có phương trình x 2 + y 2 + 2 x − 4 y − 8 = 0 là
A.M(-4;0) và M(3; 7)
B.M(1;5) và M(-2; 2)
C.M(0; 4) và M(-3; 1)
D.M(1; 5) và M(- 4; 0)
ĐÁP ÁN D
Tọa độ giao điểm của đường thẳng ∆ và đường tròn (C) nếu có là nghiệm hệ phương trình: là nghiệm của hệ phương trình
x − y + 4 = 0 ( 1 ) x 2 + y 2 + 2 x − 4 y − 8 = 0 ( 2 )
Từ (1) suy ra: y = x + 4 thay vào (2) ta được:
x 2 + ( x + 4 ) 2 + 2 x – 4 . ( x + 4 ) - 8 = 0 x 2 + x 2 + 8 x + 16 + 2 x - 4 x – 16 - 8 = 0
2x2 + 6x - 8 = 0 ⇔ x = 1 ⇒ y = 5 x = − 4 ⇒ y = 0
Vậy đường thẳng cắt đường tròn tại 2 điểm phân biệt là (1; 5) và ( -4; 0)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại A và nội tiếp trong đường tròn
(
C
)
:
x
2
+
y
2
+
2
x
-
4
y
+
1
0
và M(0;1) là trung điểm AB. Tìm tọa độ đỉnh C, biết A có hoành độ dương A. C(-1;4). B. C(1;2). C. C(-1;0). D. C(3;2).
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại A và nội tiếp trong đường tròn ( C ) : x 2 + y 2 + 2 x - 4 y + 1 = 0 và M(0;1) là trung điểm AB. Tìm tọa độ đỉnh C, biết A có hoành độ dương
A. C(-1;4).
B. C(1;2).
C. C(-1;0).
D. C(3;2).
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C):
x
2
+
y
2
-
2
x
-
4
y
+
4
0
và đường tròn (C):
x
2
+
y
2
+
6
X
+
4
y
+
4
0...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C): x 2 + y 2 - 2 x - 4 y + 4 = 0 và đường tròn (C'): x 2 + y 2 + 6 X + 4 y + 4 = 0 Tìm tâm vị tự của hai đường tròn?
A. I(0;1) và J(3;4)
B. I(-1;-2) và J(3;2)
C. I(1;2) và J(-3;-2)
D. I(1;0) và J(4;3)
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C) :
x
2
+
y
2
-
2
x
-
4
y
+
4
0
và đường tròn (C) :
x
2
+
y
2
+
6
x
+
4
y
+
4
0
Tìm tâm vị trí của hai đường tròn? A. I(0;1) và J(3;4) B. I(-1;-2) và J(3;2) C. I(1;2) và J(-3;-2) D. I(1;0...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C) : x 2 + y 2 - 2 x - 4 y + 4 = 0 và đường tròn (C') : x 2 + y 2 + 6 x + 4 y + 4 = 0 Tìm tâm vị trí của hai đường tròn?
A. I(0;1) và J(3;4)
B. I(-1;-2) và J(3;2)
C. I(1;2) và J(-3;-2)
D. I(1;0) và J(4;3)
