Tọa độ giao điểm của đường thẳng và đường tròn là nghiệm của hệ phương trình sau
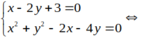
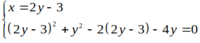
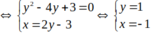 hoặc
hoặc 
Vậy tọa độ giao điểm là (3;3) và (-1; 1) .
Chọn A.
Tọa độ giao điểm của đường thẳng và đường tròn là nghiệm của hệ phương trình sau
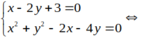
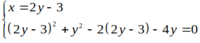
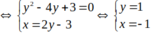 hoặc
hoặc 
Vậy tọa độ giao điểm là (3;3) và (-1; 1) .
Chọn A.
Tọa độ giao điểm của đường tròn (C): x2+ y2 – 2x -2y +1= 0 và đường thẳng ∆ : x = 1 + t y = 2 + 2 t
A. (1;2) và (2;1)
B. (1;2) và 1 5 ; 2 5
C. (2;3)
D. Đáp án khác
Cho đường tròn (C): x 2 + y 2 + 2x + 4y = 0 và đường thẳng d: 2x + y - 3 = 0. Phương trình đường thẳng d’ song song với d và tiếp xúc với đường tròn (C) là:
A. 2x + y - 1 = 0
B. 2x + y + 9 = 0
C. Cả A và B đều đúng
D. Không tồn tại đường thẳng d’
Trong mặt phẳng với hệ tọa độ Oxy. Cho đường tròn (C) : x2+ y2- 4x -2y -1= 0 và đường thẳng d: x+ y+1= 0. Tìm những điểm M thuộc đường thẳng d sao cho từ điểm M kẻ được đến (C) hai tiếp tuyến hợp với nhau góc 900.
![]()
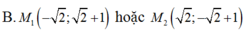
![]()
![]()
Tìm tọa độ giao điểm của đường thẳng (d): \(\left\{{}\begin{matrix}x=2+t\\y=-1+3t\end{matrix}\right.\) (t ∈ R) với đường tròn (C):x2+y2-2x-1=0
Trong mặt phẳng với hệ tọa độ cho đường tròn hai đường tròn (C): x2+ y2- 2x -2y +1= 0 và (C’) : x2+ y2+ 4x -5 = 0 cùng đi qua M( 1;0) .Viết phương trình đường thẳng d qua M cắt hai đường tròn lần lượt tại A; B sao cho MA= 2 MB.
A. 6x+ 6+ y= 0 hoặc -6x+ y- 6= 0
B. 2x+ 3y + 6= 0 hoặc 3x-2y + 3= 0
C. 2x+ y- 6= 0 hoặc x+ y- 6 = 0
D. 6x+ y – 6= 0 hoặc 6x –y-6= 0
a)Viết phương trình đường tròn đi qua 3 điểm A(-1;1);B(3;1);C(1;3)
b)Cho (C):x2+y2-4x+6y+3=0 và (Δ):3x-y+m=0.Tìm m để đường thẳng (Δ) tiếp xúc với đường tròn (C)
Cho hai điểm P(1;6) và Q(-3;-4) và đường thẳng △: 2x - y - 1 = 0.Tọa độ điểm N thuộc △ sao cho |NP - NQ| lớn nhất
A. N(-9;-19)
B. N(-1;-3)
C. M(1;1)
D. M(3;5)
Phần b và c ạ, mình cảm ơn <3
Trong mặt phẳng với hệ tọa đô Oxy , cho hai điểm A(1;1), B(4;-3) và đường
thẳng \(\Delta\) : x-2y-1=0
a) Tìm tọa độ giao điểm của đường thẳng \(\Delta\) và đường thẳng AB.
b) Tìm tọa độ điểm C thuộc đường thẳng \(\Delta\)sao cho tam giác ABC có diện tích bằng 15 .
c) Viết phương trình đường thẳng (d ) đi qua điểm D(1;4) sao cho ( d) cắt tia Ox Oy , lần lượt
tại M N , phân biệt đồng thời tổng OM + ON nhỏ nhất

Cho 2 điểm P(1;6) và Q(-3;-4) và đường thẳng △: 2x - y - 1 = 0. Tọa độ điểm M thuộc △ sao cho MP + MQ nhỏ nhất.
A. M(0;-1)
B. M(2;3)
C. M(1;1)
D. M(3;5)