Cho MA, MB là tiếp tuyến của (O). Kẻ đường kính AK của (O). BH vuông góc AK. Chứng minh KM chia đôi BH. (Dùng bổ đề hình thang để chứng minh trung điểm)

Những câu hỏi liên quan
Từ điểm M nằm ngoài (O) kẻ tiếp tuyến MA và MB với đường tròn (A,B là tiếp điểm). MO cắt AB tại I. Kẻ đường kính BC của đường tròn, MC cắt đường tròn tại điểm thứ hai là K.a, Chứng minh I là trung điểm ABb, Chứng minh MA²MK.MC và ∆MKI đồng dạng với ∆MOCc, Lấy điểm D trên cung lớn AB (DBDA), kẻ BH⊥AD tại H. Gọi E là giao điểm của MO với (O). Qua D kẻ đường thẳng vuông góc ED cắt tia BH tại P. Chứng minh BP.OAHP.OM
Đọc tiếp
Từ điểm M nằm ngoài (O) kẻ tiếp tuyến MA và MB với đường tròn (A,B là tiếp điểm). MO cắt AB tại I. Kẻ đường kính BC của đường tròn, MC cắt đường tròn tại điểm thứ hai là K.
a, Chứng minh I là trung điểm AB
b, Chứng minh MA²=MK.MC và ∆MKI đồng dạng với ∆MOC
c, Lấy điểm D trên cung lớn AB (DB<DA), kẻ BH⊥AD tại H. Gọi E là giao điểm của MO với (O). Qua D kẻ đường thẳng vuông góc ED cắt tia BH tại P. Chứng minh BP.OA=HP.OM
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN = BH.MO .
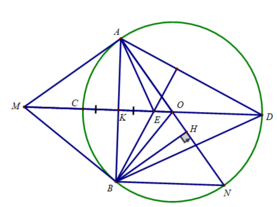
c) Ta có: ∠(ABN ) = 90 0 (B thuộc đường tròn đường kính AN)
⇒ BN // MO ( cùng vuông góc với AB)
Do đó:
∠(AOM) = ∠(ANB) (đồng vị))
∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))
⇒ ∠(ANB) = ∠(BOM)
Xét ΔBHN và ΔMBO có:
∠(BHN) = ∠(MBO ) = 90 0
∠(ANB) = ∠(BOM)
⇒ ΔBHN ∼ ΔMBO (g.g)
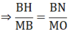
Hay MB. BN = BH. MO
Đúng 1
Bình luận (0)
cho đường tròn tâm O dây AB khác đường kính. Hai tiếp tuyến với đường tròn O tại B và tại C cắt nhau ở A.
a, Chứng minh OA là đường trung trực của BC
b, Kẻ đường kính CD kẻ BH vuông góc với CD tại H. Chứng minh BC là tia phân giác của góc ABH
c, Gọi I là giao điểm của AD và BH. Chứng minh I là trung điểm của BH
từ điểm A nằm ngoài đường trong (O) vẽ hai tiếp tuyến AB,AC với đương tròn (B,C là hai tiếp điểm ) Kẻ đường kính CD của đường tròn (O)
Chứng minh OA vuông góc BC
chứng minh BD // OA
kẻ BH vuông góc CD gọi K là giao điểm BH và AD Chứng minh K là trung điểm của BH
1.Cho tam giác ABC vuông tại A (abAC) cso AH là đường cao. Biết BH9cmHC16cma. Tính AH,ACM số đo góc ABCB. Gọi M là trung điểm của BC đường vuông góc với BC tại M cắt đường thẳng AC và BA theo thứ tự E và F. Chứng minh BH.BFMB.ABC. Gọi I là trung điểm của È.chứng minh IA là bán kính của đường tròn tâm I bán KÍNH IFD. Chứng minh MA là tiếp tuyến của đường tòn tâm Ibán kính IF2. Cho tam giấc ABC nội tiếp đường tròn (o) đườn kính BC. Vẽ dây AD của (o) vuông góc với đường kính BC tại H. Gọi M là trun...
Đọc tiếp
1.Cho tam giác ABC vuông tại A (ab<AC) cso AH là đường cao. Biết BH=9cmHC=16cm
a. Tính AH,ACM số đo góc ABC
B. Gọi M là trung điểm của BC đường vuông góc với BC tại M cắt đường thẳng AC và BA theo thứ tự E và F. Chứng minh BH.BF=MB.AB
C. Gọi I là trung điểm của È.chứng minh IA là bán kính của đường tròn tâm I bán KÍNH IF
D. Chứng minh MA là tiếp tuyến của đường tòn tâm Ibán kính IF
2. Cho tam giấc ABC nội tiếp đường tròn (o) đườn kính BC. Vẽ dây AD của (o) vuông góc với đường kính BC tại H. Gọi M là trung điểm của cạnh AC.Từ M vẽ đường thẳng vuông góc với OC, đường thẳng này cắt OI tại N trên tia ON lấy điểm S sao cho N là trung điểm của cạnh OS
A. Chứng minh tam giác ABC vuông tại A và HA=HD
B. Chứng minh MN//SC và SC là tiếp tuyến của đường trong (O)
c. Gọi K là trung điểm của cạnh HC vẽ đương tròn đường lính AH cắt cạnh AK tại F chứng minh BH. HC= À. AK
D. T rên tia đối của tia BA lấy điểm E sao hco B là trung điểm của cạnh AE chứng minh E,H,F thẳng hàng
GIÚP MÌNH VỚI!!!
cho đường tròn (O;R) , đường kính AB . kẻ tiếp tuyến Ax với đường tròn . trên tia Ax lấy điểm K(AK>R) . Qua k kẻ tiếp tuyến KM tới đường tròn (O). đường thẳng d vuông góc với AB tại O, d cắt MB tại E.
1.chứng minh KAOM là tứ giác nội tiếp
2. OK cắt AM tại I , chứng minh OI.OK=R^2
3 . gọi H là trực tâm tam giác KMA . tìm quỹ tích điểm H khi K chuyển động trên tia Ax
1: Ta có \(\widehat{KAO}=\widehat{KMO}=90^o\) nên tứ giác KAOM nội tiếp.
2: Theo hệ thức lượng trong tam giác vuông ta có \(OI.OK=OA^2=R^2\)
3: Phần thuận: Dễ thấy H thuộc KI.
Ta có \(\widehat{AHO}=90^o-\widehat{HAI}=\widehat{AMK}=\widehat{AOK}\) nên tam giác AHO cân tại A.
Do đó AH = AO = R.
Suy ra H thuộc (A; R) cố định.
Phần đảo cm tương tự.
Vậy...
Đúng 2
Bình luận (0)
Cho đường tròn (O;R) đường kính AB. Kẻ tiếp tuyến Ax với đường tròn. Trên Ax lấy điểm K(AK≥R). Qua K kẻ tiếp tuyến KM tới đường tròn(O). Đường thẳng d vuông góc với AB tại O, cắt MB tại E.
a. chứng minh 4 điểm K,A,O,M thuộc một đường tròn
b. OK cắt AM tại I, chứng minh OI.OK=OA2
a: Xét tứ giác KAOM có
\(\widehat{KAO}+\widehat{KMO}=180^0\)
Do đó: KAOM là tứ giác nội tiếp
b: Xét (O) có
KA là tiếp tuyến
KM là tiếp tuyến
Do đó: KA=KM
hay K nằm trên đường trung trực của AM(1)
Ta có: OA=OM
nên O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra OK là đường trung trực của AM
hay OK\(\perp\)AM
Xét ΔOAK vuông tại A có AI là đường cao
nên \(OI\cdot OK=OA^2\)
Đúng 1
Bình luận (0)
Bài 1: Cho ∆ABC có 3 góc nhọn nội tiếp (O;R) các đường cao BE,CF cắt nhau tại H .
a/ Chứng minh: AH vuông góc BC .
b/ AH cắt BC tại D. Kẻ đường kính AK của (O). Chứng mimh: AB.AC = 2R. AD
c/ AK cắt BC tại M. Chứng minh: MB. MC = MA. MK
d/ Gọi I là trung điểm BC. Chứng minh: H, I, K thẳng hàng
câu a) bạn sử dụng tính chất của 3 đường cao là được.
b) bạn chứng minh là tam giác ABK là tam giác vuông do chắn nửa đường tròn
sau đó xét hai tam giác vuông ACD và AKB sao cho đồng dạng : có \(\widehat{ACD}=\widehat{AKB}\)do cùng chắn cung AB
sau đó bạn suy ra tỷ số đồng dạng rồi nhân chéo là xong.
c)
bạn xét hai tam giác MAB vad MCK sao cho đồng dạng do
hai góc M bằng nhau do đối đỉnh
góc MKC= góc MBA cùng chắn cung AC
rồi suy ra 2 tam giác đó dồng dạng rồi suy ra tỉ số đồng dạng rồi nhân chéo
d câu này ta có \(\hept{\begin{cases}CF\perp AB\\KB\perp AB\end{cases}\Rightarrow CF//KB\Leftrightarrow CH//KB}\)
\(\hept{\begin{cases}BE\perp AC\\KC\perp AC\end{cases}\Rightarrow BE//CK\Leftrightarrow BH//CK}\)
TỪ 2 ĐIỀU TRÊN ta suy ra được tứ giác CHBK LÀ HÌNH BÌNH HÀNH
TỪ ĐIỀU ĐÓ SUY RA I là giao diểm của hai đường chéo suy ra i là trung điểm của HK suy ra H,I,K thằng hàng
Cho đường tròn tâm O bán kính R, dây BC khác đường kính. Hai tiếp tuyến của đường tròn (O,R) tại B và C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.
a. Chứng AO vuông góc với BC
b. Chứng minh BC là phân giác góc ABH
c. Gọi I là giao điểm của AD và BH. Chứng minh IH=IB
Bạn tự vẽ hình nhé
a.Xét 2 tam giác vuông ABO và ACO có
BO=CO (đều là BK đường tròn)
AB=AC (Độ dài hai tiếp tuyến của một đường tròn cùng xuất phát từ một điểm bên ngoài đường tròn thì bằng nhau)
góc ABO=góc ACO=90 độ
Suy ra tam giác ABO=tam giác ACo (c.g.c) suy ra góc BAO=góc CAO
Tam giác ABC cân tại A nên AO vừa là phân giác của góc BAC vừa là đường cao của tam giác ABC hạ từ A xuống BC vậy AO vuông góc với BC
b\()\)Ta có góc BCO=góc CAO (cùng phụ với góc AOC)
góc CAO=góc BAO
suy ra góc BCO=góc BAO (1)
Xét tam giác vuông BCH có góc CBH+góc BCO=90 độ (2)
Ta có góc ABC+góc BAO=90 độ (3)
Từ (1) (2) (3) suy ra góc CBH=góc ABC nên BC là phân giác của góc ABH
c,Gọi G là giao của BD và AC
\(\Delta DCG\)có OA \(//DG\)\((\)cùng \(\perp BC\)\()\); OD=OC
=> A là trung điểm của GC
Có BH//AC, theo hệ quả của định lý Thales:
\(\frac{BI}{AG}=\frac{ID}{IA}=\frac{IH}{AC}\)
=> IH=IB(đpcm)
Chúc bạn học tốt
Đúng 0
Bình luận (0)




















