a) Để A là phân số thì : \(n-2\ne0=>n\ne2\)

b) Để A nhận giá trị nguyên âm lớn nhất 

\(=>A=-1\\ =>\dfrac{n-6}{n-2}=-1\\ =>n-6=-\left(n-2\right)\\ =>n-6=-n+2\\ =>n+n=6+2\\ =>2n=8\\ =>n=4\left(TMDK\right)\)

c) \(A=\dfrac{n-6}{n-2}=\dfrac{n-2-4}{n-2}=1-\dfrac{4}{n-2}\)

Để A nhận gt số nguyên thì : \(\dfrac{4}{n-2}\in Z=>4⋮\left(n-2\right)\\ =>n-2\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\\ =>n\in\left\{3;1;4;0;6;-2\right\}\)

Đến đây bạn lập bảng giá trị rồi thay từng gt n vào bt A, giá trị nào cho A là STN thì bạn nhận gt đó ạ.

d) Mình nghĩ bạn thiếu đề ạ 

Bài 1: Ta có:

\(M=\frac{ad}{abcd+abd+ad+d}+\frac{bad}{bcd.ad+bc.ad+bad+ad}+\frac{c.abd}{cda.abd+cd.abd+cabd+abd}+\frac{d}{dab+da+d+1}\)

\(=\frac{ad}{1+abd+ad+d}+\frac{bad}{d+1+bad+ad}+\frac{1}{ad+d+1+abd}+\frac{d}{dab+da+d+1}\)

$=\frac{ad+abd+1+d}{ad+abd+1+d}=1$

Bài 2:

Vì $a,b,c,d\in [0;1]$ nên

\(N\leq \frac{a}{abcd+1}+\frac{b}{abcd+1}+\frac{c}{abcd+1}+\frac{d}{abcd+1}=\frac{a+b+c+d}{abcd+1}\)

Ta cũng có:
$(a-1)(b-1)\geq 0\Rightarrow a+b\leq ab+1$

Tương tự:

$c+d\leq cd+1$

$(ab-1)(cd-1)\geq 0\Rightarrow ab+cd\leq abcd+1$

Cộng 3 BĐT trên lại và thu gọn thì $a+b+c+d\leq abcd+3$

$\Rightarrow N\leq \frac{abcd+3}{abcd+1}=\frac{3(abcd+1)-2abcd}{abcd+1}$

$=3-\frac{2abcd}{abcd+1}\leq 3$

Vậy $N_{\max}=3$

3.

Hình vẽ:

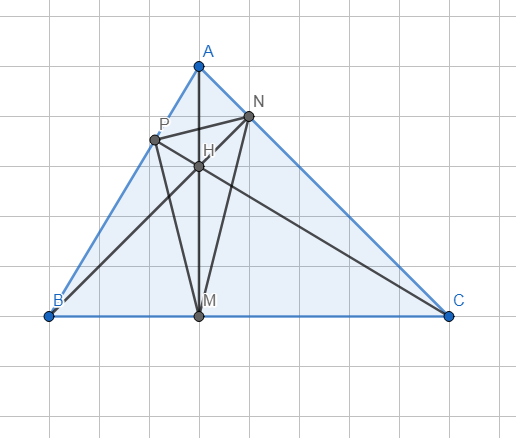
Lời giải:

a) △AMC và △BNC có: \(\widehat{AMC}=\widehat{BNC}=90^0;\widehat{ACB}\) là góc chung.

\(\Rightarrow\)△AMC∼△BNC (g-g).

\(\Rightarrow\dfrac{AC}{BC}=\dfrac{CM}{CN}\Rightarrow AC.CN=BC.CM\left(1\right)\)

b) △AMB và △CPB có: \(\widehat{AMB}=\widehat{CPB}=90^0;\widehat{ABC}\) là góc chung.

\(\Rightarrow\)△AMB∼△CPB (g-g)

\(\Rightarrow\dfrac{AB}{CB}=\dfrac{BM}{BP}\Rightarrow AB.BP=BC.BM\left(2\right)\)

Từ (1) và (2) suy ra:

\(AC.CN+AB.BP=BC.CM+BC.BM=BC.\left(CM+BM\right)=BC.BC=BC^2\left(đpcm\right)\)b) Gọi \(M_0\) là trung điểm BC, giả sử \(AB< AC\).

\(\widehat{HBM}=90^0-\widehat{BHM}=90^0-\widehat{AHN}=\widehat{CAM}\)

△HBM và △CAM có: \(\widehat{HBM}=\widehat{CAM};\widehat{HMB}=\widehat{CMA}=90^0\)

\(\Rightarrow\)△HBM∼△CAM (g-g) 

\(\Rightarrow\dfrac{MH}{CM}=\dfrac{BM}{MA}\Rightarrow MH.MA=BM.CM\)

Ta có: \(BM.CM=\left(BM_0-MM_0\right)\left(CM_0+MM_0\right)=\left(BM_0-MM_0\right)\left(BM_0+MM_0\right)=BM_0^2-MM_0^2\le BM_0^2=\dfrac{BC^2}{4}\)

\(\Rightarrow MH.MA\le\dfrac{BC^2}{4}\).

Vì \(BC\) không đổi nên: \(max\left(MH.MA\right)=\dfrac{BC^2}{4}\), đạt được khi △ABC cân tại A hay A nằm trên đường trung trực của BC.

c) Sửa đề: \(S_1.S_2.S_3\le\dfrac{1}{64}.S^3\)

△AMC∼△BNC \(\Rightarrow\dfrac{AC}{BC}=\dfrac{MC}{NC}\Rightarrow\dfrac{AC}{MC}=\dfrac{BC}{NC}\)

△ABC và △MNC có: \(\dfrac{AC}{MC}=\dfrac{BC}{NC};\widehat{ACB}\) là góc chung.

\(\Rightarrow\)△ABC∼△MNC (c-g-c)

\(\Rightarrow\dfrac{S_{MNC}}{S_{ABC}}=\dfrac{S_1}{S}=\dfrac{MC}{AC}.\dfrac{NC}{BC}\left(1\right)\)

Tương tự: 

△ABC∼△MBP \(\Rightarrow\dfrac{S_{MBP}}{S_{ABC}}=\dfrac{S_2}{S}=\dfrac{MB}{AB}.\dfrac{BP}{BC}\left(2\right)\)

△ABC∼△ANP \(\Rightarrow\dfrac{S_{ANP}}{S_{ABC}}=\dfrac{S_3}{S}=\dfrac{AN}{AB}.\dfrac{AP}{AC}\left(3\right)\)

Từ (1), (2), (3) suy ra:

\(\dfrac{S_1}{S}.\dfrac{S_2}{S}.\dfrac{S_3}{S}=\left(\dfrac{MC}{AC}.\dfrac{NC}{BC}\right).\left(\dfrac{MB}{AB}.\dfrac{BP}{BC}\right).\left(\dfrac{AN}{AB}.\dfrac{AP}{AC}\right)\) 

\(\Rightarrow\dfrac{S_1}{S}.\dfrac{S_2}{S}.\dfrac{S_3}{S}=\left(\dfrac{MC.MB}{AC.AB}\right).\left(\dfrac{BP.AP}{AC.BC}\right).\left(\dfrac{AN.CN}{AB.BC}\right)\) (*)

Áp dụng câu b) ta có:

\(\left\{{}\begin{matrix}BM.CM\le\dfrac{1}{4}BC^2\\AP.BP\le\dfrac{1}{4}AB^2\\AN.CN\le\dfrac{1}{4}AC^2\end{matrix}\right.\)

Từ (*) suy ra:

\(\dfrac{S_1}{S}.\dfrac{S_2}{S}.\dfrac{S_3}{S}\le\left(\dfrac{\dfrac{1}{4}BC^2}{AC.AB}\right).\left(\dfrac{\dfrac{1}{4}AC^2}{AC.BC}\right).\left(\dfrac{\dfrac{1}{4}AB^2}{AB.BC}\right)=\dfrac{1}{64}\)

\(\Rightarrow S_1.S_2.S_3\le\dfrac{1}{64}.S^3\)

Dấu "=" xảy ra khi △ABC đều.

Mn ơi ai bt làm câu nào thì giúp mik cậu đó với !!

1. a. 

Ta có: 12⁸ = (12⁴)² = 20736²

Ta thấy: 20736 > 81

=> 12⁸ > 81²

(Các câu khác cũng tương tự nhé.)