1. Cho \(\Delta ABC\) đều có cạnh là a. Tính diện tích \(\Delta ABC\) theo a.
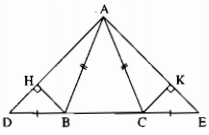
2. Cho \(\Delta ABC\) cân tại A. Trên tia đối của tia BC lấy điểm D, tia đối của CB lấy điểm E sao cho BD = CE. M là trung điểm của BC.
a) C/m AM là phân giác \(\widehat{DAE}\)
b) Vẽ \(BK\perp AD\left(K\in AD\right)\), \(CF\perp AE\left(F\in AE\right)\) . C/m 3 đường thẳng AM, BK, CF cùng đi qua một điểm.
3. Cho \(\widehat{xOy}\) = 1200. A là điểm thuộc tia phân giác của \(\widehat{xOy}\) . Vẽ \(AB\perp Ox\), \(AC\perp Oy\) .
a) \(\Delta ABC\) là tam giác gì?
b) C/m \(OA\perp BC\)
4. Cho \(\Delta ABC\) , tia phân giác của \(\widehat{ABC}\) cắt AC tại D. Qua D kẻ Dx // AB, Dx cắt BC tại M. Gọi My là tia phân giác \(\widehat{DMC}\) , Bz là tia phân giác ngoài của \(\widehat{B}\) . C/m \(Bz\perp My\) .
5. Cho \(\Delta ABC\) cân tại A, AB = 5cm, BC = 8cm. Kẻ \(AH\perp BC\left(H\in BC\right)\) .
a) C/m HB = HC
b) Tính AH
c) Kẻ \(HD\perp AB,HE\perp AC\) . C/m \(\Delta HDE\) cân.
6. Cho \(\widehat{xOy}\) nhọn. I là một điểm điểm thuộc tia phân giác của \(\widehat{xOy}\) . Kẻ \(IA\perp Ox,IB\perp Oy\)
a) C/m IA = IB. Biết OI = 10cm, AI = 6cm. Tính OA.
b) Gọi K là giao điểm của BI \(\cap\) Ox, M là giao điểm của AI \(\cap\) Oy. So sánh AK và BM.
c) Gọi C là giao điểm của OI và MK. C/m OC \(\perp\) MK