a) Cho hình bình hành ABCD. Gọi O là một điểm trong hình bình hành. Chứng minh SAOB + SCOD = SBOC + SAOD
b) Cho hình thang ABCD (AB // CD). Gọi O là giao điểm hai đường chéo. Chứng minh SAOD = SBOC
Cho hình thang ABCD(AB//CD),hai đường chéo cắt nhau tại O
a,CMR SAOD=SBOC
b,Cho biết SAOB=9,SCOD=25 tính SABCD
Cho hình thang ABCD(AB//CD). Gọi Ơ là giao điểm hai đường chéo, Sabc=a, Scdo= b. a. Chứng minh Saod= Sbco b. Tính Saod
Ta thấy tam giác ACD và tam giác BCD có chung đáy cd , chiều cao bằng nhau và bằng chiều cao hình thang ABCD . Nên Sacd=Sbcd. Suy ra Saod=Sboc
b) cho diện tích abo=a thì chắc mình mới làm được nhé....
Xét tam giác aob và cod có
aob=cod (đối đỉnh), abo=cdo(so le trong do ab//cd)
Suy ra 2 tam giác này đồng dạng
=> (Ao/oc)^2=Saob/Scod=a/b
Xét tam giác aod và cdo chung đường cao hạ từ d xuống ac. Suy ra Saod/Scod=ao/co= căn (a/b)
=> Saod= căn (a/b) * b= căn (ab)
Cho hình thang ABCD có đáy AB,AC cắt BD tại O
a.Hãy chứng tỏ Saod=Sboc
b.Tìm tỷ số độ dài của đoạn thẳng BO và OD
C.CHo Saob=36 cm mét vuông và Scod=64 cm mét vuông.Tính diện tích hình thang ABCD
CHO HÌNH BÌNH HÀNH ABCD có E là trung điểm AD,F là trung điểm CD gọi O là giao điểm hai đường chéo . chứng minh ÈOD là hình bình hành
Xét ΔADC có
O là trung điểm của AC
E là trung điểm của AD
Do đó: OE là đường trung bình của ΔADC
Suy ra: OE//DF và OE=DF
hay OEDF là hình bình hành
cho tứ giác ABCD. Gọi O là giao điểm của các đường thẳng nối trung điểm những cạnh đối diện. chứng minh rằng
SAOD + SBOC = 1/2 SABCD
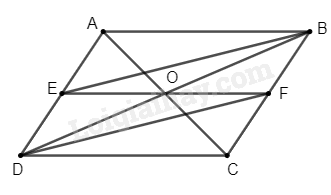
Cho hình bình hành \(ABCD\). Gọi \(E\) là trung điểm của \(AD\), \(F\) là trung điểm của \(BC\)
a) Chứng minh rằng tứ giác \(EBFD\) là hình bình hành
b) Gọi \(O\) là giao điểm của hai đường chéo của hình bình hành \(ABCD\). Chứng minh rằng ba điểm \(E\), \(O\), \(F\) thẳng hàng.
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Mà \(E\), \(F\) là trung điểm của \(AD\), \(BC\) (gt)
Suy ra \(AE = ED = BF = FC\)
Xét tứ giác \(EBFD\) ta có:
\(ED = FB\) (cmt)
\(ED\) // \(BF\) (do \(AD\) // \(BC\))
Suy ra \(EDFB\) là hình bình hành
b) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Mà \(DEBF\) là hình bình hành (gt)
Suy ra \(O\) cũng là trung điểm của \(EF\)
Suy ra \(E\), \(O\), \(F\) thẳng hàng
Cho hình thang ABCD, qua giao điểm O của 2 đường chéo kẻ đường song song với đấy, cắt AB, BC tại E, G.C/m Saod=Sboc và OE=OG
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Gọi M, N lần lượt là trung điểm OB, OD
a) Chứng minh AMCN là hình bình hành
b) Hình bình hành ABCD cần có thêm điều kiện gì để AMCN là hình chữ nhật
c) AN cắt CD tại E, CM cắt AB tại tâm O. Chứng minh rằng E và F đối xứng với nhau qua tâm O
Cho hình bình hành ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Qua điểm O, vẽ đường thẳng a cắt hai đường thẳng AD, BC lần lượt tại E, F. Qua O vẽ đưòng thẳng b cắt hai cạnh AB, CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành
Ta có DAOK = DCOH Þ OK =OH, DDOE = DBOF Þ OE = OF Þ EHFK là hình bình hành

. Cho hình bình hành ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Qua điểm O, vẽ đường thẳng a cắt hai đường thẳng AD, BC lần lượt tại E, F, vẽ đường thẳng b cắt hai cạnh AB, CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔOAK và ΔOCH có
\(\widehat{OAK}=\widehat{OCH}\)(hai góc so le trong, AK//CH)
OA=OC
\(\widehat{AOK}=\widehat{COH}\)(hai góc đối đỉnh)
Do đó: ΔOAK=ΔOCH
=>OK=OH
=>O là trung điểm của KH
Xét ΔOAE và ΔOCF có
\(\widehat{EAO}=\widehat{FCO}\)(hai góc so le trong, AE//CF)
OA=OC
\(\widehat{AOE}=\widehat{COF}\)
Do đó: ΔOAE=ΔOCF
=>OE=OF
=>O là trung điểm của EF
Xét tứ giác EKFH có
O là trung điểm chung của EF và KH
=>EKFH là hình bình hành