ĐKXĐ: x<>-1

Để \(\dfrac{3x^2}{x+1}\in Z\) thì \(3x^2⋮x+1\)

=>\(3x^2-3+3⋮x+1\)

=>\(3⋮x+1\)

=>\(x+1\in\left\{1;-1;3;-3\right\}\)

=>\(x\in\left\{0;-2;2;-4\right\}\)

b) Tìm x nguyên để A nguyên

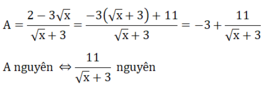
⇔ x  + 3 ∈ Ư(11) ⇔ x + 3 ∈ {-11; -1; 1; 11}

Do  x  + 3 ≥ 3 nên  x  + 3 = 11 ⇔  x  = 8 ⇔ x = 64

Vậy với x = 64 thì A nguyên

a) \(ĐKXĐ:\hept{\begin{cases}3x\ne0\\x+1\ne0\\2-4x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne0\\x\ne-1\\x\ne\frac{1}{2}\end{cases}}\)

     \(A=\left(\frac{x+2}{3x}+\frac{2}{x+1}-3\right):\frac{2-4x}{x+1}-\frac{3x+1-x^2}{3x}\)

          \(=\left[\frac{\left(x+1\right)\left(x+2\right)}{3x\left(x+1\right)}+\frac{6x}{3x\left(x+1\right)}-\frac{9x\left(x+1\right)}{3x\left(x+1\right)}\right]:\frac{2\left(1-2x\right)}{x+1}-\frac{3x+1-x^2}{3x}\)

       \(=\frac{\left(x+1\right)\left(x+2\right)+6x-9x\left(x+1\right)}{3x\left(x+1\right)}.\frac{x+1}{2\left(1-2x\right)}-\frac{3x+1-x^2}{3x}\)

       \(=\frac{2-8x^2}{3x\left(x+1\right)}.\frac{x+1}{2\left(1-2x\right)}-\frac{3x+1-x^2}{3x}\)

      \(=\frac{1+2x-3x-1+x^2}{3x}\)

      \(=\frac{x\left(x-1\right)}{3x}=\frac{x-1}{3}\)

b)\(\text{Với }x\ne0,x\ne-1,x\ne\frac{1}{2}\text{ ta có:}\)

  \(\text{Để A< 0\Leftrightarrow}\frac{x-1}{3}< 0\Rightarrow x-1< 0\Leftrightarrow x< 1\)

Dựa theo kết quả câu  a)   mk lm tiếp câu  b)   nhé:

b)  ĐKXĐ:  \(x\ne0;\)\(x\ne-1;\)\(x\ne0,5\)

 \(A< 0\) thì   \(\frac{x-1}{3}< 0\)

  \(\Leftrightarrow\)\(x-1< 0\)   (do  \(3>0\))

\(\Leftrightarrow\)\(x< 1\)

Vậy  với    \(x< 1\)thỏa mãn  ĐKXĐ   thì   \(A< 0\)

a)

ĐKXĐ: \(x\notin\left\{0;3;-3\right\}\)

Ta có: \(A=\left(\dfrac{1}{3}+\dfrac{3}{x^2-3x}\right):\left(\dfrac{x^2}{27-3x^2}+\dfrac{1}{x+3}\right)\)

\(=\left(\dfrac{1}{3}+\dfrac{3}{x\left(x-3\right)}\right):\left(\dfrac{-x^2}{3\left(x-3\right)\left(x+3\right)}+\dfrac{1}{x+3}\right)\)

\(=\left(\dfrac{x\left(x-3\right)}{3x\left(x-3\right)}+\dfrac{9}{3x\left(x-3\right)}\right):\left(\dfrac{-x^2}{3\left(x-3\right)\left(x+3\right)}+\dfrac{3\left(x-3\right)}{3\left(x-3\right)\left(x+3\right)}\right)\)

\(=\dfrac{x^2-3x+9}{3x\left(x-3\right)}:\dfrac{-x^2+3x-9}{3\left(x-3\right)\left(x+3\right)}\)

\(=\dfrac{x^2-3x+9}{3x\left(x-3\right)}\cdot\dfrac{3\left(x-3\right)\left(x+3\right)}{-\left(x^2-3x+9\right)}\)

\(=\dfrac{-x-3}{x}\)

b) Để A nguyên thì \(-x-3⋮x\)

mà \(-x⋮x\)

nên \(-3⋮x\)

\(\Leftrightarrow x\inƯ\left(-3\right)\)

\(\Leftrightarrow x\in\left\{1;-1;3;-3\right\}\)

Kết hợp ĐKXĐ, ta được: \(x\in\left\{1;-1\right\}\)

Vậy: Để A nguyên thì \(x\in\left\{1;-1\right\}\)

a) \(\dfrac{2x+5}{2x+1}=\dfrac{2x+1+4}{2x+1}=\dfrac{2x+1}{2x+1}+\dfrac{4}{2x+1}=1+\dfrac{4}{2x+1}\)  

Để \(\dfrac{2x+5}{2x+1}\in Z\) thì \(\dfrac{4}{2x+1}\in Z\) 

\(\Rightarrow4\) ⋮ \(2x+1\)

\(\Rightarrow2x+1\inƯ\left(4\right)=\left\{1;-1;2;-2;4;-4\right\}\)

\(\Rightarrow2x\in\left\{0;-2;1;-3;3;-5\right\}\)

\(\Rightarrow x\in\left\{0;-1;\dfrac{1}{2};-\dfrac{3}{2};\dfrac{3}{2};-\dfrac{5}{2}\right\}\)

Mà x nguyên \(\Rightarrow\text{x}\in\left\{0;-1\right\}\) 

b) \(\dfrac{3x+5}{x+1}=\dfrac{3x+3+2}{x+1}=\dfrac{3\left(x+1\right)+2}{x+1}=\dfrac{3\left(x+1\right)}{x+1}+\dfrac{2}{x+1}=3+\dfrac{2}{x+1}\) 

Để \(\dfrac{3x+5}{x+1}\in Z\) thì \(\dfrac{2}{x+1}\in Z\) 

\(\Rightarrow2\) ⋮ \(x+1\)

\(\Rightarrow x+1\inƯ\left(2\right)=\left\{1;-1;2;-2\right\}\)

\(\Rightarrow x\in\left\{0;-2;1;-3\right\}\) 

c) \(\dfrac{3x+8}{x-1}=\dfrac{3x-3+11}{x-1}=\dfrac{3\left(x-1\right)+11}{x-1}=\dfrac{3\left(x-1\right)}{x-1}+\dfrac{11}{x-1}=3+\dfrac{11}{x-1}\)  

Để: \(\dfrac{3x+8}{x-1}\in Z\) thì \(\dfrac{11}{x-1}\in Z\)

\(\Rightarrow11\) ⋮ \(x-1\)

\(\Rightarrow x-1\inƯ\left(11\right)=\left\{1;-1;11;-11\right\}\)

\(\Rightarrow x\in\left\{2;0;12;-10\right\}\)

d) \(\dfrac{5x+12}{x-2}=\dfrac{5x-10+22}{x-2}=\dfrac{5\left(x-2\right)+22}{x-2}=\dfrac{5\left(x-2\right)}{x-2}+\dfrac{22}{x-2}=5+\dfrac{22}{x-2}\)

Để: \(\dfrac{5x+12}{x-2}\in Z\) thì \(\dfrac{22}{x-2}\in Z\)

\(\Rightarrow22\) ⋮ \(x-2\)

\(\Rightarrow x-2\inƯ\left(22\right)=\left\{1;-1;2;-2;11;-11;22;-22\right\}\)

\(\Rightarrow x\in\left\{3;1;4;0;13;-9;24;-20\right\}\)

e) \(\dfrac{7x-12}{x+16}=\dfrac{7x+112-124}{x+16}=\dfrac{7\left(x+16\right)-124}{x+16}=\dfrac{7\left(x+16\right)}{x+16}-\dfrac{124}{x+16}=7-\dfrac{124}{x+16}\)

Để \(\dfrac{7x-12}{x+16}\in Z\) thì \(\dfrac{124}{x+16}\in Z\) 

\(\Rightarrow124\) ⋮ \(x+16\)

\(\Rightarrow x+16\inƯ\left(124\right)=\left\{1;-1;2;-2;4;-4;31;-31;62;-62;124;-124\right\}\)

\(\Rightarrow x\in\left\{-15;-17;-14;-18;-12;-20;15;-47;46;-78;108;-140\right\}\)