\(f'\left(x\right)=\left(sin^2x\right)'+4\cdot\left(sinx'\right)-5'\)

\(=2\cdot sinx\cdot cosx+4\cdot cosx=2cosx\left(sinx+2\right)\)

\(f'\left(x\right)=0\)

=>\(cosx\left(sinx+2\right)=0\)

=>\(cosx=0\)

=>\(x=\dfrac{\Omega}{2}+k\Omega\)

mà \(x\in\left[0;\dfrac{\Omega}{2}\right]\)

nên \(x=\dfrac{\Omega}{2}\)

\(f\left(\dfrac{\Omega}{2}\right)=sin^2\left(\dfrac{\Omega}{2}\right)+4\cdot sin\left(\dfrac{\Omega}{2}\right)-5\)

=1+4-5=0

\(f\left(0\right)=sin^20+4\cdot sin0-5=-5\)

=>Chọn D

-1 ≥ 3 – 4sinx ≥ 7

1: Ta có: \(-1<=\sin\left(2x+\frac{\pi}{4}\right)\le1\)

=>\(-3\le3\cdot\sin\left(2x+\frac{\pi}{4}\right)\le3\)

=>\(-3-1\le3\cdot\sin\left(2x+\frac{\pi}{4}\right)-1\le3-1\)

=>-4<=y<=2

=>Tập giá trị là T=[-4;2]

\(y_{\min}=-4\) khi \(\sin\left(2x+\frac{\pi}{4}\right)=-1\)

=>\(2x+\frac{\pi}{4}=-\frac{\pi}{2}+k2\pi\)

=>\(2x=-\frac34\pi+k2\pi\)

=>\(x=-\frac38\pi+k\pi\)

2: \(0\le cos^2x\le1\)

=>\(0\ge-5\cdot cos^2x\ge-5\)

=>\(0+3\ge-5\cdot cos^2x+3\ge-5+3\)

=>3>=y>=-2

=>Tập giá trị là T=[-2;3]

\(y_{\max}=3\) khi \(cos^2x=1\)

=>\(\sin^2x=0\)

=>sin x=0

=>\(x=k\pi\)

\(y_{\min}=-2\) khi \(cos^2x=0\)

=>cosx=0

=>\(x=\frac{k\pi}{2}\)

3: \(-1\le cosx\le1\)

=>\(-3\le3\cdot cosx\le3\)

=>\(-3+4\le3\cdot cosx+4\le3+4\)

=>\(1\le3\cdot cosx+4\le7\)

=>\(\frac51\ge\frac{5}{3\cdot cosx+4}\ge\frac57\)

=>\(\frac57\le y\le5\)

=>Tập giá trị là \(T=\left\lbrack\frac57;5\right\rbrack\)

\(y_{\min}=\frac57\) khi cosx=1

=>\(x=k2\pi\)

\(y_{\max}=5\) khi cosx=-1

=>\(x=\pi+k2\pi\)

4: \(y=\sin^2x-4\cdot\sin x+8\)

\(=\sin^2x-4\cdot\sin x+4+4\)

\(=\left(\sin x-2\right)^2+4\)

Ta có: \(-1\le\sin x\le1\)

=>\(-1-2\le\sin x-2\le1-2\)

=>\(-3\le\sin x-2\le-1\)

=>\(1\le\left(\sin x-2\right)^2\le9\)

=>\(5\le\left(\sin x-2\right)^2+4\le13\)

=>5<=y<=13

=>Tập giá trị là T=[5;13]

\(y_{\min}=5\) khi sin x-2=-1

=>sin x=1

=>\(x=\frac{\pi}{2}+k2\pi\)

\(y_{\max}\) =13 khi sin x-2=-3

=>sin x=-1

=>\(x=-\frac{\pi}{2}+k2\pi\)

Đặt \(sin^24x=t\left(t\in\left[0;1\right]\right)\)

\(y=1-8sin^22x.cos^22x+2sin^42x\)

\(=1-2sin^24x+2sin^42x\)

\(\Rightarrow y=f\left(t\right)=1-2t+2t^2\)

\(y_{min}=min\left\{f\left(0\right);f\left(1\right);f\left(\dfrac{1}{2}\right)\right\}=\dfrac{1}{2}\)

\(y_{max}=max\left\{f\left(0\right);f\left(1\right);f\left(\dfrac{1}{2}\right)\right\}=1\)

Ta có : y = sin²x – 4sinx – 5= (sinx- 2)² -  9

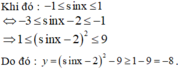
Vậy giá trị nhỏ nhất của hàm số là - 8

Đáp án B

Đặt \(sinx=t\in\left[-1;1\right]\)

\(y=f\left(t\right)=t^2+2t\)

Xét hàm \(y=f\left(t\right)=t^2+2t\) trên \(\left[-1;1\right]\)

\(-\dfrac{b}{2a}=-1\in\left[-1;1\right]\)

\(f\left(-1\right)=-1\) ; \(f\left(1\right)=3\)

\(\Rightarrow y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)

\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)