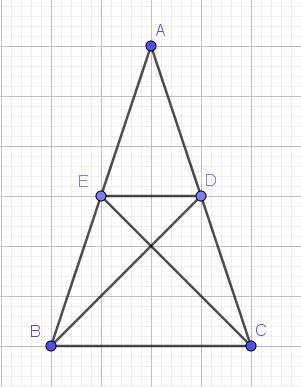
cho tam giác ABC cân tại A . Gọi BD, CE là các đường trung tuyến
a) chứng minh BEDC là hình thang cân
b) BD cắt CE tại O . Gọi F, H lần lượt là trung điểm BO và CO . chứng minh DEFH là hình chữ nhật
c) AO cắt BC tại I . chứng minh OFIH là hình thoi
help me ![]()