AB//DE. chứng minh rằng AC song song với CD

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB AC Gọi I là trung điểm của BC D là trung điểm của AC a chứng minh tam giác amb bằng tam giác ABC và AE vuông góc với BC b từ A kẻ đường thẳng vuông góc với BD cắt BC tại D trên tia đối của tia de lấy điểm F sao cho de AB Chứng minh rằng tam giác ADM bằng C D E Từ đó suy ra AE AB song song với CD e từ C kẻ đường thẳng vuông góc với AC cắt tại g Chứng minh tam giác ABD bằng tam giác ABC Chứng minh rằng AB ACG
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = AC Gọi I là trung điểm của BC D là trung điểm của AC a chứng minh tam giác amb bằng tam giác ABC và AE vuông góc với BC b từ A kẻ đường thẳng vuông góc với BD cắt BC tại D trên tia đối của tia de lấy điểm F sao cho de = AB Chứng minh rằng tam giác ADM bằng C D E Từ đó suy ra AE = AB song song với CD e từ C kẻ đường thẳng vuông góc với AC cắt tại g Chứng minh tam giác ABD bằng tam giác ABC Chứng minh rằng AB = ACG
cho tam giác ABC (AB<AC), các phân giác BD,CE
a, đường thẳng qua D và song song với BC cắt AB ở K. Chứng minh rằng E nằm giữa B và K
b, Chứng minh rằng CD>DE>BE
a) Theo tinh chat phan giac ta co :
AD/CD = AB/BC (1)
BE/AE = BC/AC (2)
Lay (1) x (2) : (AD/CD)(BE/AE) = AB/AC < 1 ( vi AB < AC)
<=> AD/CD < AE/BE
<=> AK/BK < AE/BE ( do KD//BC => AD/CD = AK/BK)
<=> (AB - BK)/BK < (AB - BE)/BE
<=> AB/BK - 1 < AB/BE - 1
<=> AB/BK < AB/BE <=> 1/BK < 1/BE
<=> BK > BE => E nam giua B va K (dpcm)
b) Theo ket qua cau a) => ^EDB < ^KDB = ^CBD ( so le trong vi KD//BC) = ^EBD ( vi BB la phan giac) => BE < ED (3) ( trong tg doi dien voi goc be hon la canh be hon)
Tuong tu nhu the neu ke EF//BC ( F thuoc AC ) => F nam giua C va D do do ta cung co ^DCE = ^BCE = ^FEC < ^DEC => ED < CD (4)
Tu (3) va (4) co : BE < ED < CD ( dpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC cân tại A. Lấy E, D theo thứ tự thuộc AC, AB, BE cắt CD tại O. Chứng minh rằng
a, BE=CD
b, DE song song BC
c, tam giác OBD = tam giác OCE
sai đề rồi bạn ơi, đãng lẽ phải là lấy E và D là tđ chứ
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB, kẻ tia Ax bất kỳ, lấy các điểm C, D, E sao cho AC = CD = DE. Qua C, D kẻ đường thẳng song song với BE. Chứng minh rằng đoạn thẳng AB bị chia ra ba phân bằng nhau.
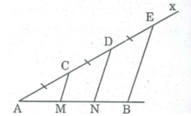
Gọi giao điểm của các đường thẳng kẻ từ C và D song song với BE cắt AB tại M và N.
Ta có: AC = CD = DE (gt)
CM // DN // BE
Theo tính chất đường thẳng song song cách đều, ta có:
AM = MN = NB
Đúng 0
Bình luận (0)
Cho tam giác ABC, đường phân giác AD, D thuộc BC. Qua D kẻ DE song song với AC(E thuộc AB)
a, Chứng minh tam giác AED cân
b, Chứng minh CD.BE=DB.DE
c, Gọi O là giao điểm của AD và EC. Từ O kẻ đường thẳng song song với AC. Đường thẳng này cắt CD tại M. Chứng minh rằng: ED.AC=DM.AC+OM.ED
a: Xét ΔEAD có \(\widehat{EAD}=\widehat{EDA}\)
nên ΔEAD cân tại E
b: Xét ΔABC có AD là phân giác
nên DC/DB=AC/AB(1)
Xét ΔABC có DE//AC
nên DE/BE=AC/AB(2)
Từ (1) và (2) suy ra DC/DB=DE/BE
hay \(DC\cdot BE=DE\cdot BD\)
Đúng 0
Bình luận (0)
cho hình vẽ . chứng minh AB song song với CD B A E C D 100 độ 120 độ 140 độ
cho tam giác ABC có trung tuyến AK. Một đường thẳng song song với BC vá cắt AB và AK và AC lấn lượt tại M, I và N
a) chứng minh MI=NI
b)các tia phân giác của góc AIM,AIN cắt AB và AC lần lượt tại D và E. Chứng minh DE song song với BC
c) gọi O là giao điểm của BE và CD. Chứng minh rằng 3 điểm A,O,K thẳng hàng
Cho tam giác ABC
a/ Qua D là trung điểm của cạnh AB kẻ DE song song với BC (E thuộc AC) . Chứng minh: EA=EC
b/Nếu D và C lần lượt là trung điểm của AB và AC . Chứng minh: DE song song với BC
Liên Hồng Phúc nó tương tự chứ ko có giống hết ![]()
Đúng 0
Bình luận (0)
Bài toán 7 : Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến AM,
qua H kẻ đường thẳng song song với AB cắt AC tại D. Qua H kẻ đường thẳng
song song với AC cắt AB tại E.
1. Chứng minh rằng : AH = DE.
2. Chứng minh rằng : AM DE.
3. ABC cần có thêm điều kiện gì để tứ giác AEHD là hình vuông.
4. Cho AB = 6cm, AC = 8cm. Tính diện tích tứ giác AEMD.
Cm: a) Ta có: BA ⊥⊥AC (gt)
HD // AB (gt)
=> HD ⊥⊥AC => ˆHDA=900HDA^=900
Ta lại có: AC ⊥⊥AB (gt)
HE // AC (gt)
=> HE ⊥⊥AB => ˆHEA=900HEA^=900
Xét tứ giác AEHD có: ˆA=ˆAEH=ˆHDA=900A^=AEH^=HDA^=900
=> AEHD là HCN => AH = DE
b) Gọi O là giao điểm của AH và DE
Ta có: AEHD là HCN => OE = OH = OD = OA
=> t/giác OAD cân tại O => ˆOAD=ˆODAOAD^=ODA^ (1)
Xét t/giác ABC vuông tại A có AM là đường trung tuyến
-> AM = BM = MC = 1/2 BC
=> t/giác AMC cân tại M => ˆMAC=ˆCMAC^=C^
Ta có: ˆB+ˆC=900B^+C^=900 (phụ nhau)
ˆC+ˆHAC=900C^+HAC^=900 (phụ nhau)
=> ˆB=ˆHACB^=HAC^ hay ˆB=ˆOADB^=OAD^ (2)
Từ (1) và (2) => ˆODA=ˆBODA^=B^
Gọi I là giao điểm của MA và ED
Xét t/giác IAD có: ˆIAD+ˆIDA+ˆAID=1800IAD^+IDA^+AID^=1800 (tổng 3 góc của 1 t/giác)
=> ˆAID=1800−(IAD+ˆIDA)AID^=1800−(IAD+IDA^)
hay ˆAID=1800−(ˆB+ˆC)=1800−900=900AID^=1800−(B^+C^)=1800−900=900
=> AM⊥DEAM⊥DE(Đpcm)
c) (thiếu đề)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có góc B = góc C bằng 40 độ. Kẻ phân giác BD ( D thuộc AC). Trên tia AB lấy điểm M sao cho AM = BC. Từ D dựng đường thẳng song song với BC cắt AB tại E.
a) Chứng minh DE = CD
b) Chứng minh BD + AD = BC
c) tính góc AMC























