cấu tạo của cân thăng bằng

Những câu hỏi liên quan
Đặt lên hai đĩa cân những quả cân như Hình 1.
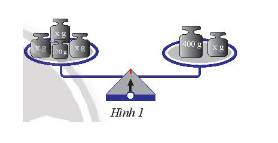
a) Biết rằng cân thăng bằng, hãy viết phương trình biểu thị sự thăng bằng này.
b) Nếu \(x = 100\) cân có thăng bằng không? Vì sao?
Nếu \(x = 150\) thì cân có thăng bằng không? Vì sao?
Từ đó, chỉ ra một nghiệm của phương trình ở câu a.
a) Trên đĩa cân bên trái ta thấy có 4 quả cân, có 3 quả có khối lượng \(x\) gam và 1 quả có khối lượng 100 gam nên khối lượng đĩa cân bên trái là: \(x + x + x + 100\) (gam)
Trên đĩa cân bên phải ta thấy có 2 quả cân, 1 quả có khối lượng \(x\) gam và một quả có khối lượng 400 gam nên khối lượng đĩa cân bên phải là: \(x + 400\) gam.
Từ điều kiện cân thăng bằng ta có biểu thức mối quan hệ sau:
\(x + x + x + 100 = x + 400\) hay \(3x + 100 = 400 + x\).
Vậy phương trình biểu diễn sự thăng bằng là \(3x + 100 = 400 + x\).
b) Nếu \(x = 100\) thì khối lượng đĩa cân bên trái là: \(3.100 + 100 = 300 + 100 = 400\) (gam); khối lượng đĩa cân bên phải là \(400 + 100 = 500\) (gam).
Do đó, cân không thăng bằng.
Nếu \(x = 150\) thì khối lượng đĩa cân bên trái là: \(3.150 + 100 = 550\) (gam); khối lượng đĩa cân bên phải là \(150 + 400 = 550\) (gam).
Do đó, cân thăng bằng.
Đúng 0
Bình luận (0)
Khi cân một bao đầu bằng cân Rôbecvan, người ta đã dùng một quả cân 3kg, một quả cân 500g nhưng cân vẫn mất thăng bằng do đĩa chứa các quả cân nặng hơn. Để cân thăng bằng, người ta phải bỏ vào đĩa cân có bao đậu một quả cân 50g. Khối lượng của bao đậu là:
A. 3,45kg.
B. 3405g.
C. 3,5kg.
D. 3550g.
Khi cân một bao sỏi bằng cân Robecvan, một nhóm học sinh đã đặt 2 quả cân 2kg, 1 quả cân 500g và 1 quả cân 200g vào đĩa cân bên phải thì cân vẫn mất thăng bằng. Nhưng khi đặt 1 quả cân 50g vào đĩa cân bên trái có bao sỏi thì cân thăng bằng. khối lượng của bao sỏi là
A. 4,7 kg
B. 4,5 kg
C. 4,75 kg
D. 4,65 kg
Khối lượng của các quả cân ở đĩa bên phải là
2.2 + 1.0,5 + 1.0,2 = 2,7 (kilogam)
Khối lượng của bao sỏi và quả cân ở đĩa bên trái là:
P + 0,05 (kg)
⇔ Khối lượng bao sỏi + 0,05 = 2,7
⇒ khối lượng bao sỏi = 2,7 – 0,05 = 2,65 (kg)
VẬY KHỐI LƯỢNG BAO SỎI BẰNG 2,65KG
Trên cùng một đĩa cân đã thăng bằng có một cốc đựng 200g dung dịch axit HCl 10%, một miếng đá vôi (CaCO3) và một cục kẽm. Bỏ lần lượt miếng đá vôi và cục kẽm dung dịch. Sau phản ứng người ta thấy còn một ít kẽm không tan. Muốn cho cân trở lại thăng bằng người ta phải đặt thêm vào đĩa cân có khối lượng 9 g. Hãy xác định nồng độ phần trăm của muối trong dung dịch mới tạo thành.
Đọc tiếp
Trên cùng một đĩa cân đã thăng bằng có một cốc đựng 200g dung dịch axit HCl 10%, một miếng đá vôi (CaCO3) và một cục kẽm. Bỏ lần lượt miếng đá vôi và cục kẽm dung dịch. Sau phản ứng người ta thấy còn một ít kẽm không tan. Muốn cho cân trở lại thăng bằng người ta phải đặt thêm vào đĩa cân có khối lượng 9 g.
Hãy xác định nồng độ phần trăm của muối trong dung dịch mới tạo thành.
Khi cho đá vôi và Zn vào dd HCl có các phản ứng sau xảy ra:
2HCl + CaCO3 ---> CaCl2 + H2O + CO2
2HCl + Zn ---> ZnCl2 + H2
Số mol HCl ban đầu = 10.200/100.36,5 = 0,548 mol.
Khối lượng 9g là khối lượng hụt đi do CO2 và H2 bay ra.
Gọi x, y tương ứng là số mol của CaCl2 và ZnCl2. Ta có: x + y = nHCl/2 = 0,274 và 44x + 2y = 9
Giải hệ thu được x = 0,2; y = 0,074.
Đúng 0
Bình luận (0)
Nhưng mak còn lại 1 ít Zn mak
Vs lại tại sao x+y= l\(\frac{n_{HCL}}{2}\)
Đúng 0
Bình luận (0)
Dùng cân Rôbécvan có đòn cân phụ để cân một vật. Khi cân thăng bằng thì khối lượng của vật bằng: A. giá trị của số chỉ của kim trên bẳng chia độ B. giá trị của số chỉ của con mã trên đòn cân phụ C. tổng khối lượng của các quả cân đặt trên đĩa D. tổng khối lượng của các quả cân đặt trên đĩa cộng với giá trị của số chỉ của con mã
Đọc tiếp
Dùng cân Rôbécvan có đòn cân phụ để cân một vật. Khi cân thăng bằng thì khối lượng của vật bằng:
A. giá trị của số chỉ của kim trên bẳng chia độ
B. giá trị của số chỉ của con mã trên đòn cân phụ
C. tổng khối lượng của các quả cân đặt trên đĩa
D. tổng khối lượng của các quả cân đặt trên đĩa cộng với giá trị của số chỉ của con mã
Chọn D
Dùng cân Rôbécvan có đòn cân phụ để cân một vật. Khi cân thăng bằng thì khối lượng của vật bằng tổng khối lượng của các quả cân đặt trên đĩa cộng với giá trị của số chỉ của con mã.
Đúng 0
Bình luận (0)
Câu 1: Cho 28 (g) Fe tác dụng với 2,479) khi C*l_{2} a cân bằng ptpu theo pp thăng bằng electron b. Tính khối lượng muối tạo thành ? giải.
a)
| $Fe^0 \to Fe^{+3} + 3e$ | x2 |
| $Cl_2 + 2e \to 2Cl^-$ | x3 |
$2Fe + 3Cl_2 \xrightarrow{t^o} 2FeCl_3$
b)
$n_{Fe} = \dfrac{28}{56} = 0,5(mol)$
$n_{Cl_2} = \dfrac{2,479}{24,79} = 0,1(mol)$
Ta thấy :
$n_{Fe} :2>n_{Cl_2}:3$ nên $Fe$ dư
$n_{FeCl_3} = \dfrac{2}{3}n_{Cl_2} = \dfrac{0,2}{3}(mol)$
$\Rightarrow m_{FeCl_3} = \dfrac{0,2}{3}.162,5 = 10,83(gam)$
Đúng 2
Bình luận (0)
Dùng cân Rô – béc – van có đòn cân phụ để cân một vật. Khi cân thăng bằng thì khối lượng của vật bằng: A. giá trị của số chỉ của kim trên bảng chia độ. B. giá trị của số chỉ của con mã trên đòn cân phụ. C. tổng khối lượng của các quả cân trên đĩa. D. tổng khối lượng của các quả cân đặt trên đĩa cộng với giá trị của số chỉ của con mã.
Đọc tiếp
Dùng cân Rô – béc – van có đòn cân phụ để cân một vật. Khi cân thăng bằng thì khối lượng của vật bằng:
A. giá trị của số chỉ của kim trên bảng chia độ.
B. giá trị của số chỉ của con mã trên đòn cân phụ.
C. tổng khối lượng của các quả cân trên đĩa.
D. tổng khối lượng của các quả cân đặt trên đĩa cộng với giá trị của số chỉ của con mã.
Dùng cân Rô – béc – van có đòn cân phụ để cân một vật. Khi cân thăng bằng thì khối lượng của vật bằng tổng khối lượng của các quả cân đặt trên đĩa cộng với giá trị của số chỉ của con mã.
⇒ Đáp án D
Đúng 0
Bình luận (0)
Dùng cân Rô-béc-van có đòn cân phụ đế cân một vật. Khi cân thăng bằng thì khối lượng của vật bằng: A. Giá trị số chỉ của kim trên bảng chia độ B. Giá trị của số chỉ con mã trên đòn cân phụ C. Tổng khối lượng của các quả cân đặt trên đĩa D. Tổng khối lượng của các quả cân đặt trên đĩa cộng với giá trị khối lượng ứng với chỉ số chỉ của con mã
Đọc tiếp
Dùng cân Rô-béc-van có đòn cân phụ đế cân một vật. Khi cân thăng bằng thì khối lượng của vật bằng:
A. Giá trị số chỉ của kim trên bảng chia độ
B. Giá trị của số chỉ con mã trên đòn cân phụ
C. Tổng khối lượng của các quả cân đặt trên đĩa
D. Tổng khối lượng của các quả cân đặt trên đĩa cộng với giá trị khối lượng ứng với chỉ số chỉ của con mã
Cách dùng cân Rô-béc-van: Đặt vật đem cân lên đĩa cân bên trái, đặt lên đĩa cân bên kia một số quả cân có khối lượng phù hợp sao cho đòn cân nằm thăng bằng, kim cân nằm đúng giữa bảng chia độ. Khi đó, khối lượn của vật bằng tổng khối lượng của các quả cân đặt trên đĩa cộng với giá trị khối lượng ứng với số chỉ của con mã.
Đáp án: D
Đúng 0
Bình luận (0)
hai quả cầu, một bằng bạc, một thủy tinh có cùng khối lượng m được treo vào hai đĩa của một cân đòn. Khi nhúng ngập quả cầu vào nước, cân mất thăng bằng. Để cân trở lại thăng bằng , ta phải thêm một quả cân có khối lượng m1 21 g vào đĩa cân có quả cầu bạc.a) Nếu nhúng ngập quả cầu thủy tinh vào nước thì khối lượng quả cân m2 cần đặt vào bên đĩa có quả cầu thủy tinh là bao nhiêu để cân trở lại thăng bằng? Biết khối lượng riêng của bạc, thủy tinh và nước lần lượt là 10500 kg/m3, 2500kg/m3,1000kg/m...
Đọc tiếp
hai quả cầu, một bằng bạc, một thủy tinh có cùng khối lượng m được treo vào hai đĩa của một cân đòn. Khi nhúng ngập quả cầu vào nước, cân mất thăng bằng. Để cân trở lại thăng bằng , ta phải thêm một quả cân có khối lượng m1= 21 g vào đĩa cân có quả cầu bạc.
a) Nếu nhúng ngập quả cầu thủy tinh vào nước thì khối lượng quả cân m2 cần đặt vào bên đĩa có quả cầu thủy tinh là bao nhiêu để cân trở lại thăng bằng? Biết khối lượng riêng của bạc, thủy tinh và nước lần lượt là 10500 kg/m3, 2500kg/m3,1000kg/m3
b) Nếu nhúng cả hai quả cầu vào dầu có khối lượng riêng 800kg/m3 thì cần đặt thêm quả cân có khối lượng m3 bằng bao nhiêu và vào bên nào


















