\(\overrightarrow{MN}=k\overrightarrow{PQ}\)\(\Rightarrow\)MN song song với PQ

Những câu hỏi liên quan
Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {MN} = 2\overrightarrow {PQ} \)
B. \(\overrightarrow {MN} = 2\overrightarrow {NP} \)
C. \(\overrightarrow {MN} = - 2\overrightarrow {PQ} \)
D. \(\overrightarrow {MQ} = - 2\overrightarrow {NP} \)
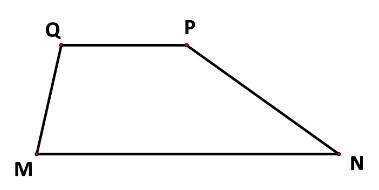
Do MQ và PN không song song với nhau nên \(\overrightarrow {MQ} \ne k\overrightarrow {NP} \). Vậy loại B và D.
Ta có: \(\overrightarrow {MN} ,\overrightarrow {PQ} \)là hai vecto ngược hướng và \(\left| {\overrightarrow {MN} } \right| = 2\left| {\overrightarrow {PQ} } \right|\)
Suy ra \(\overrightarrow {MN} = - 2\overrightarrow {PQ} \)
Vậy chọn C.
Đúng 1
Bình luận (0)
Cho M,N,P,Q
C/m nếu :
a) \(\overrightarrow{MN}=\overrightarrow{PQ}\)thì \(\overrightarrow{MP}=\overrightarrow{NQ}\)
b) \(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}\)
c) \(\overrightarrow{MN}+\overrightarrow{PQ}=\overrightarrow{MQ}+\overrightarrow{PN}\)
Cm
1) overrightarrow{PQ}+overrightarrow{NP}+overrightarrow{MN}overrightarrow{MQ}
2)overrightarrow{NP}+overrightarrow{MN}overrightarrow{QP}+overrightarrow{MQ}
3)overrightarrow{MN}+overrightarrow{PQ}overrightarrow{MQ}+overrightarrow{PN}
4)overrightarrow{MN}+overrightarrow{PQ}+overrightarrow{QM}+overrightarrow{NP}overrightarrow{O}
5)overrightarrow{AB}-overrightarrow{CD}overrightarrow{AC}+overrightarrow{DB}
6)overrightarrow{AD}+overrightarrow{BE}+overrightarrow{CF}overrightarrow{AE}+overrighta...
Đọc tiếp
Cm
1) \(\overrightarrow{PQ}+\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{MQ}\)
2)\(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}\)
3)\(\overrightarrow{MN}+\overrightarrow{PQ}=\overrightarrow{MQ}+\overrightarrow{PN}\)
4)\(\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{QM}+\overrightarrow{NP}=\overrightarrow{O}\)
5)\(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{DB}\)
6)\(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{BF}\)
7)\(\overrightarrow{AD}-\overrightarrow{FC}-\overrightarrow{EB}=\overrightarrow{CD}-\overrightarrow{EA}-\overrightarrow{FB}\)
8)\(\overrightarrow{AB}-\overrightarrow{DC}-\overrightarrow{FE}=\overrightarrow{CF}-\overrightarrow{DA}+\overrightarrow{EC}\)
1. Cho tứ giác MNPQ. CMR:
a) \(\overrightarrow{PQ}+\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{MQ}\)
b)\(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}\)
Dễ mà bạn :)) cái này dùng qui tắc công với chèn điểm là nuột =)
a) \(\overrightarrow{PQ}+\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{NP}+\overrightarrow{PQ}+\overrightarrow{MN}\)
\(=\overrightarrow{NQ}+\overrightarrow{MN}=\overrightarrow{MN}+\overrightarrow{NQ}=\overrightarrow{MQ}\left(đpcm\right)\)
( quá chi tiết rồi nha bạn... )
b) Ta có: \(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{MQ}+\overrightarrow{QN}\)
\(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}+\overrightarrow{NQ}+\overrightarrow{QN}\)
\(\Rightarrow\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Dựng \(\overrightarrow{AM}=\overrightarrow{BA};\overrightarrow{MN}=\overrightarrow{DA};\overrightarrow{NP}=\overrightarrow{DC};\overrightarrow{PQ}=\overrightarrow{BC}\). Chứng minh \(\overrightarrow{AQ}=\overrightarrow{0}\) ?
Do \(\overrightarrow{NP}=\overrightarrow{DC}\); \(\overrightarrow{AM}=\overrightarrow{BA}\Rightarrow\overrightarrow{MA}=\overrightarrow{AB}\).
Do tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB}=\overrightarrow{DC}\).
Vì vậy \(\overrightarrow{NP}=\overrightarrow{MA}\) nên tứ giác NPAM là hình bình hành.
Vì vậy \(\overrightarrow{PA}=\overrightarrow{NM}\). (1)
Mà \(\overrightarrow{MN}=\overrightarrow{DA}\) suy ra \(\overrightarrow{NM}=\overrightarrow{AD}\) . (2)
Mặt khác \(\overrightarrow{AD}=\overrightarrow{BC}\) (do tứ giác ABCD là hình bình hành). (3)
Từ (1);(2);(3) suy ra:\(\overrightarrow{PA}=\overrightarrow{BC}\).
Mà \(\overrightarrow{PQ}=\overrightarrow{BC}\Rightarrow\overrightarrow{PQ}=\overrightarrow{PA}\).
Vì vậy hai điểm A và Q trùng nhau nên \(\overrightarrow{AQ}=\overrightarrow{0}\).
Đúng 0
Bình luận (0)
Cho hình thang MNPQ (MN // PQ) có MP = NQ. Qua N kẻ đường thảng song song vói MP, cắt đường thẳng PQ tại K chứng minh: tam giác NKQ là tam giác cân cho hình thang MNPQ ( MN song song PQ) có MP = NQ . Qua N kẻ đường thảng song song vs MP , cắt đường thẳng PQ tại Kchứng minh: a) tam giác NKQ là tam giác cân b) tam giác MPQ = tam giác NQP c) MNPQ lằ hình thang cân
a: Xét tứ giác MNKP có
MN//KP
MP//NK
=>MNKP là hình bình hành
=>MP=NK
mà MP=NQ
nên NK=NQ
=>ΔNKQ cân tại N
b: MNKP là hbh
=>góc K=góc NMP
=>góc K=góc MPQ
=>góc MPQ=góc NQP
Xét ΔMQP và ΔNPQ có
MP=NQ
góc MPQ=góc NQP
QP chung
=>ΔMQP=ΔNPQ
c: ΔMQP=ΔNPQ
=>góc MQP=góc NPQ
=>MNPQ là hình thang cân
Đúng 3
Bình luận (0)
Cho đường tròn (O; 25cm).Hai dây MN và PQ song song với nhau và có độ dài theo thứ tự bằng 40cm,48cm (MN và PQ nằm khác phía so với điểm O).Tính khoảng cách giữa hai dây MN và PQ
Cho hình tứ diện ABCD. Gọi M. N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng :
a) \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}=2\overrightarrow{MN}\)
b) \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}-\overrightarrow{BD}=2\overrightarrow{PQ}\)
Rút gọn các biểu thức sau
a. overrightarrow{OM}-overrightarrow{ON}+overrightarrow{AD}+overrightarrow{MD}+overrightarrow{EK}-overrightarrow{EP}-overrightarrow{MD}
b. overrightarrow{AB}+overrightarrow{MN}-overrightarrow{CB}+overrightarrow{PQ}+overrightarrow{CA}+overrightarrow{NM}
c. overrightarrow{KM}+overrightarrow{DF}+overrightarrow{AC}-overrightarrow{KF}+overrightarrow{CD}-overrightarrow{AP}+overrightarrow{MP}
Đọc tiếp
Rút gọn các biểu thức sau
a. \(\overrightarrow{OM}-\overrightarrow{ON}+\overrightarrow{AD}+\overrightarrow{MD}+\overrightarrow{EK}-\overrightarrow{EP}-\overrightarrow{MD}\)
b. \(\overrightarrow{AB}+\overrightarrow{MN}-\overrightarrow{CB}+\overrightarrow{PQ}+\overrightarrow{CA}+\overrightarrow{NM}\)
c. \(\overrightarrow{KM}+\overrightarrow{DF}+\overrightarrow{AC}-\overrightarrow{KF}+\overrightarrow{CD}-\overrightarrow{AP}+\overrightarrow{MP}\)























