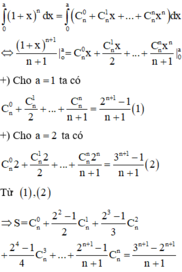Chứng minh rằng1/22+1/23+1/24+...+1/2n <1

Những câu hỏi liên quan
Chứng minh rằng
1) ( 88 + 220 ) ⋮ 17
2) A = 2 + 22 + 23 + … + 2120 chia hết cho cả 3; 7 và 15.
\(1,8^8+2^{20}=2^{24}+2^{20}=2^{20}\left(2^4+1\right)=2^{20}\cdot17⋮17\)
\(2,A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{119}+2^{120}\right)\\ A=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{119}\left(1+2\right)\\ A=3\left(2+2^3+...+2^{119}\right)⋮3\)
\(A=\left(2+2^2+2^3\right)+...+\left(2^{118}+2^{119}+2^{120}\right)\\ A=2\left(1+2+2^2\right)+...+2^{118}\left(1+2+2^2\right)\\ A=\left(1+2+2^2\right)\left(2+...+2^{118}\right)=7\left(2+...+2^{118}\right)⋮7\\ A=\left(2+2^2+2^3+2^4\right)+...+\left(2^{117}+2^{118}+2^{119}+2^{120}\right)\\ A=2\left(1+2+2^2+2^3\right)+...+2^{117}\left(1+2+2^2+2^3\right)\\ A=\left(1+2+2^2+2^3\right)\left(2+...+2^{117}\right)=15\left(2+...+2^{117}\right)⋮15\)
Đúng 2
Bình luận (0)
Mọi người giải giúp em với ạ. Em đang cần gấp !!!
Đúng 0
Bình luận (0)
Chứng minh: 1/21+ 1/22+ 1/23+ 1/24+ ... + 1/80 không phải là số tự nhiên
chứng minh 1/21 + 1/22 + 1/23 + 1/24 +...........+ 1/80 không phải số tự nhiên giải được cho 5 sao và câu trả lời hay nhất - câu hỏi 1862868
bạn tham khảo lời giải nha
Đúng 0
Bình luận (0)
Chứng minh A = 1 + 2 + 22 + 23 + 24 +…+ 219 + 220.chứng tỏ rằng A chia hết cho 3
A=\((1+2)+\left(2^2+2^3\right)+...+\left(2^{19}+2^{20}\right)\)
A=\(3.1+2^2\left(1+2\right)+...+2^{19}\left(1+2\right)\)
A=\(3.1+3.2^2+...+3.2^{19}\)
A=\(3\left(1+2^2+...+2^{19}\right)\)\(⋮3\)
Vậy A\(⋮3\)
Đúng 1
Bình luận (0)
A=(1+2)+(22+23)+...+(219+220)(1+2)+(22+23)+...+(219+220)
A=3.1+22(1+2)+...+219(1+2)3.1+22(1+2)+...+219(1+2)
A=3.1+3.22+...+3.2193.1+3.22+...+3.219
A=3(1+22+...+219)3(1+22+...+219)⋮3⋮3
NÊN A⋮3
Đúng 1
Bình luận (0)
Chứng minh: \(\dfrac{1}{21}\)+\(\dfrac{1}{22}\)+\(\dfrac{1}{23}\)+\(\dfrac{1}{24}\)+....+\(\dfrac{1}{80}\)không phải là một số tự nhiên.
Chứng minh S = 1/21 + 1/22 + 1/23 + 1/24 + .... + 1/80 không phải là một số tự nhiên.
Giúp mình câu này đi, mình cần gấp lắm, ai đúng mình k cho.
Cho biểu thức: A= 1/21 + 1/22 + 1/23 + 1/24 +...+ 1/40
Chứng minh rằng 1/2<A<1
Số số hạng của biểu thức A là: (40-21):1+1=20(số hạng)
Ta có : 1/21>1/40,1/22>1/40,1/23>1/40,...,1/40=1/40
1/21+1/22+1/23+...+1/40>1/40+1/40+1/41+1/40+...+1/40( 20 số 1/40)
A>1/40x20=1/2
A>1/20 (1)
Lại có: 1/21=1/21,1/21>1/22,1/21>1/23,...,1/21>1/40
1/21+1/21+1/21+...+1/21(20 số 1/21)>1/21+1/22+1/23+...+1/40
1/21x20>A
20/21>A.Mà 1>20/21
1>A (2)
Từ (1) và (2) ta có : 1/2<A<1(đpcm)
Vậy bài tôán đđcm
Đúng 1
Bình luận (0)
\(\frac{1}{2}=\frac{1}{40}+\frac{1}{40}+....+\frac{1}{40}\)có 20 số hạng \(\)
\(\frac{1}{21}+\frac{1}{22}+....+\frac{1}{40}\)có 20 số hạng
\(\frac{1}{21}>\frac{1}{40}\)
\(\frac{1}{22}>\frac{1}{40}\)
\(.....\)
\(\frac{1}{40}=\frac{1}{40}\)\(\Rightarrow\frac{1}{2}< \frac{1}{21}+\frac{1}{22}+.....+\frac{1}{40}\)
\(1=\frac{1}{40}+....+\frac{1}{40}\)có 40 số hạng mà A chỉ có 20 số hạng
\(\Rightarrow\frac{1}{2}< A< 1\)
Đúng 0
Bình luận (0)
Cho A = 1 + 2 + 22 + 23 + 24 +…299 Chứng minh rằng: A không chia hết cho 7
A=(1+2+2^2)+2^3(1+2+2^2)+...+2^96(1+2+2^2)+2^99
=7(1+2^3+...+2^96)+2^99 ko chia hết cho 7
Đúng 0
Bình luận (0)
Chứng minh rằng: 1/5+1/20+1/21+1/22+1/23+1/24+1/25+1/101+1/102+1/103+1/104 +1/105<1/2
1/5+(1/20+1/21+1/22+1/23+1/24+1/25)+(1/101+1/102+103+104+105) Ta thấy 1/21;1/22;1/23;1/24;1/25 đều nhỏ hơn 1/20 nên 1/21+1/22+1/23+1/24+1/25<5×1/20<1/4 Tương tự 1/101+1/102+1/103+1/104+1/105<5×1/100<1/20 1/5+1/20+1/20=6/20=3/10 1/5+(<1/4)+(<1/20)<1/2 1/2=5/10 3/10<5/10 vậy suy ra điều cần chứng minh
Đúng 0
Bình luận (0)
Chứng minh rằng: 1/5+1/20+1/21+1/22+1/23+1/24+1/25+1/101+1/102+1/103+1/104 +1/105<1/2
1/5+(1/20+1/21+1/22+1/23+1/24+1/25)+(1/101+1/102+103+104+105)
Ta thấy 1/21;1/22;1/23;1/24;1/25 đều nhỏ hơn 1/20 nên
1/21+1/22+1/23+1/24+1/25<5×1/20<1/4
Tương tự
1/101+1/102+1/103+1/104+1/105<5×1/100<1/20
1/5+1/20+1/20=6/20=3/10
1/5+(<1/4)+(<1/20)<1/2
1/2=5/10
3/10<5/10 vậy suy ra điều cần chứng minh
Đúng 0
Bình luận (0)
Tính tổng
S C
n
0
+
2
2
−
1
2
C
n
1
+
2
3
−
1
3
C
n
2
+
2...
Đọc tiếp
Tính tổng S = C n 0 + 2 2 − 1 2 C n 1 + 2 3 − 1 3 C n 2 + 2 4 − 1 4 C n 3 + ... + 2 n + 1 − 1 n + 1 C n n
A. S = 3 n + 2 − 2 n + 2 n + 2
B. S = 3 n + 1 − 2 n + 1 n + 1
C. S = 3 n + 2 + 2 n + 2 n + 2
D. S = 3 n + 1 + 2 n + 1 n + 1