Cho tam giác ABC nhọn. Chứng minh rằng
\(BC^2\)=\(AB^2+AC^2-2AB.AC.cosA\) (định lí cosin)
Cho tam giác ABC nhọn. Chứng minh rằng
\(BC^2\)=\(AB^2+AC^2-2AB.AC.cosA\) (định lí cosin)
Kẻ đường cao \(BH\).
Xét tam giác \(ABH\)vuông tại \(H\):
\(BH^2=AB^2-AH^2\)
Xét tam giác \(BCH\)vuông tại \(H\):
\(BH^2=BC^2-CH^2=BC^2-\left(AC-AH\right)^2\)
\(=BC^2-AC^2+2AC.AH-AH^2\)
\(\Rightarrow BC^2-AC^2+2AC.AH-AH^2=AB^2-AH^2\)
\(\Leftrightarrow BC^2=AB^2+AC^2-2AC.AH=AB^2+AC^2-2AC.ABcosA\)
* Cho tam giác nhọn ABC. CM: \(BC^2=AB^2+AC^2-2AB.AC.cosA\)
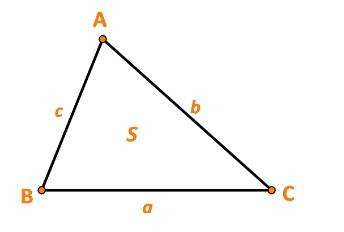
Cho tam giác ABC có BC = a, AC = b, AB =c và diện tích là S. (Hình 24).
a) Từ định lí cosin, chứng tỏ rằng:
\(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \) ở đó \(p = \frac{{a + b + c}}{2}\)
b) Bằng cách sử dụng công thức \(S = \frac{1}{2}bc\sin A\),hãy chứng tỏ rằng: \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
Áp dụng định lí cosin trong tam giác ABC ta có:
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\)\( \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \(\sin A = \sqrt {1 - {{\cos }^2}A} \).
\( \Rightarrow \sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}} = \sqrt {\frac{{{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}}}{{{{(2bc)}^2}}}} \)
\( \Leftrightarrow \sin A = \frac{1}{{2bc}}\sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)
Đặt \(M = \sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)
\(\begin{array}{l} \Leftrightarrow M = \sqrt {(2bc + {b^2} + {c^2} - {a^2})(2bc - {b^2} - {c^2} + {a^2})} \\ \Leftrightarrow M = \sqrt {\left[ {{{(b + c)}^2} - {a^2}} \right].\left[ {{a^2} - {{(b - c)}^2}} \right]} \\ \Leftrightarrow M = \sqrt {(b + c - a)(b + c + a)(a - b + c)(a + b - c)} \end{array}\)
Ta có: \(a + b + c = 2p\)\( \Rightarrow \left\{ \begin{array}{l}b + c - a = 2p - 2a = 2(p - a)\\a - b + c = 2p - 2b = 2(p - b)\\a + b - c = 2p - 2c = 2(p - c)\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow M = \sqrt {2(p - a).2p.2(p - b).2(p - c)} \\ \Leftrightarrow M = 4\sqrt {(p - a).p.(p - b).(p - c)} \\ \Rightarrow \sin A = \frac{1}{{2bc}}.4\sqrt {p(p - a)(p - b)(p - c)} \\ \Leftrightarrow \sin A = \frac{2}{{bc}}.\sqrt {p(p - a)(p - b)(p - c)} \end{array}\)
b) Ta có: \(S = \frac{1}{2}bc\sin A\)
Mà \(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \)
\(\begin{array}{l} \Rightarrow S = \frac{1}{2}bc.\left( {\frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} } \right)\\ \Leftrightarrow S = \sqrt {p(p - a)(p - b)(p - c)} .\end{array}\)
Cho tam giác ABC nhọn. Chứng minh rằng cosA + cosB + cosC = AB^2 + AC^2 + BC^2/4.S.ABC
Xét tam giác ABC nhọn có \(BC^2=AB^2+AC^2-2AB\cdot AC\cdot\cos\widehat{A}\)
\(\Rightarrow\cos\widehat{A}=\dfrac{AB^2+AC^2-BC^2}{2AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4\cdot\dfrac{1}{2}AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4S_{ABC}}\)
Cmtt: \(\left\{{}\begin{matrix}\cos\widehat{B}=\dfrac{AB^2+BC^2-AC^2}{4S_{ABC}}\\\cos\widehat{C}=\dfrac{AC^2+BC^2-AB^2}{4S_{ABC}}\end{matrix}\right.\)
\(\Rightarrow\cos\widehat{A}+\cos\widehat{B}+\cos\widehat{C}\\
=\dfrac{AB^2+AC^2-BC^2+AB^2+BC^2-AC^2+AC^2+BC^2-AB^2}{4S_{ABC}}\\
=\dfrac{AB^2+AC^2+BC62}{4S_{ABC}}\)
Cho tam giác ABC nhọn biết góc A = 60 độ . Chứng minh rằng BC^2 = AB^2 +AC^2 - AB.AC
Cho tam giác ABC nhọn biết góc A = 60 độ . Chứng minh rằng BC^2 = AB^2 +AC^2 - AB.AC
cho tam giác ABC nhọn
chứng minh rằng AC^2=AB^2+BC^2-2AB*BC*cosB
CAMON CÁC BẠN
cho tam giác ABC nhọn
chứng minh rằng : AB2=AC2 +BC2-2.AC.BC.cosC
đây là định lý cosin lớp 10
a2 = b2+c2 - 2bccosa
b2 = a2+c2 - 2accosb
c2 = a2+b2 -2abcosc
cho tam giác ABC nhọn. Kẻ AH vuông góc BC tại H. Chứng minh rằng AB^2+CH^2=AC^2+BH^2. Giúp mình với ạ
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=CH^2+AH^2\)
hay \(CH^2=AC^2-AH^2\)
Ta có: \(AB^2+CH^2=AH^2+BH^2+AC^2-AH^2\)
nên \(AB^2+CH^2=AC^2+BH^2\)(đpcm)