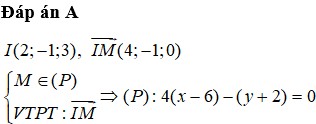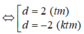VIẾT phương trình mặt phẳng địa điểm M(2;-5;3) và song song với mặt phẳng (xOz)

Những câu hỏi liên quan
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 0 và đường thẳng d có phương trình:
x
12
+
4
t
y
9
+
3
t
z...
Đọc tiếp
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 = 0 và đường thẳng d có phương trình: x = 12 + 4 t y = 9 + 3 t z = 1 + t
Viết phương trình mặt phẳng β chứa điểm M và vuông góc với đường thẳng d.
(β) vuông góc với d
⇒ (β) nhận vtcp của d 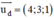 là 1 vtpt.
là 1 vtpt.
(β) đi qua M(0; 0; -2)
⇒ (β): 4x + 3y + z + 2 = 0.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho điểm M (1;1;-2) và mặt phẳng (α) : x - y - 2z = 2. Viết phương trình mặt cầu (S) có tâm M tiếp xúc với mặt phẳng (α)
Lời giải:
Bán kính mặt cầu là:
\(R=d(M, (a))=\frac{|1-1-2(-2)-2|}{\sqrt{1^2+1^2+2^2}}=\frac{\sqrt{6}}{3}\)
PT mặt cầu $(S)$ là:
$(x-1)^2+(y-1)^2+(z+2)^2=\frac{2}{3}$
Đúng 0
Bình luận (0)
Hãy viết phương trình mặt phẳng (α) đi qua điểm M(2; -1; 2) và song song với mặt phẳng (β) : 2x – y + 3z + 4 = 0
Vì mặt phẳng (α) song song với mặt phẳng ( β) : 2x – y + 3z + 4 = 0 nên phương trình của mp(α) có dạng 2x – y + 3z + D = 0
Vì M(2; -1; 2) ∈ mp(α) nên 4 + 1 + 6 + D = 0 <=> D = -11
Vậy phương trình của mp(α) là: 2x – y + 3z - 11= 0
Đúng 0
Bình luận (0)
Viết phương trình mặt phẳng chứa trục Ox và chứa điểm M(4; -1; 2)
A. 2y + z = 0
B. 4x + 3y = 0
C. 3x + z = 0
D. 2y – z = 0
Viết phương trình của mặt phẳng ( β ) đi qua điểm M(2; -1; 2), song song với trục Oy và vuông góc với mặt phẳng ( α ): 2x – y + 3z + 4 = 0
Mặt phẳng ( β ) song song với trục Oy và vuông góc với mặt phẳng ( α ):
2x – y + 3z + 4 = 0, do đó hai vecto có giá song song hoặc nằm trên ( β ) là: j → = (0; 1; 0) và n α → = (2; −1; 3)
Suy ra ( β ) có vecto pháp tuyến là n β → = j → ∧ n α → = (3; 0; −2)
Mặt phẳng ( β ) đi qua điểm M(2; -1; 2) có vecto pháp tuyến là: n β → = (3; 0; −2)
Vậy phương trình của ( β ) là: 3(x – 2) – 2(z – 2) = 0 hay 3x – 2z – 2 = 0
Đúng 0
Bình luận (0)
Viết phương trình mặt phẳng tiếp xúc với mặt cầu
(
S
)
:
(
x
-
2
)
2
+
(
y
+
1
)
2
+
(
z
-
3
)...
Đọc tiếp
Viết phương trình mặt phẳng tiếp xúc với mặt cầu ( S ) : ( x - 2 ) 2 + ( y + 1 ) 2 + ( z - 3 ) 2 = 9 tại điểm M(6; -2; 3).
A. 4x-y-26=0
B. 4x+y-26=0
C. 4x+y+26=0
D. 4x-y+26=0
Trong mặt phẳng Oxy,cho đường tròn (C) có phương trình (x-3)2+(y+1)2=10.Viết phương trình tiếp tuyến cua đường tròn đã cho tại điểm M∈(C),biết hoành độ của điểm M là X0=2
+
Gọi \(M\left(2;y_M\right)\) là tiếp điểm của (C):
\(\Leftrightarrow2^2+y_M^2-12+2y_M=0\)
\(\Leftrightarrow y_M^2+2y_M-8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y_M=2\\y_M=-4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}M\left(2;2\right)\\M\left(2;-4\right)\end{matrix}\right.\)
* Với M(2;2)
Ta có: \(\overrightarrow{u}=\overrightarrow{IE}=\left(-1;3\right)\Rightarrow\overrightarrow{n}=\left(3;1\right)\)
\(\Rightarrow\left(D\right):3x+y-8=0\)
* Với M(2; -4)
Ta có: \(\overrightarrow{u}=\overrightarrow{IE}=\left(-1;-3\right)\Rightarrow\overrightarrow{n}=\left(-3;1\right)\)
\(\Rightarrow\left(D\right):-3x+y+4=0\)
Đúng 2
Bình luận (0)
Cho mặt phẳng (Q): x - y + 2z - 2 0. Viết phương trình mặt phẳng (P) song song với mặt phẳng (Q), đồng thời cắt các trục Ox, Oy lần lượt tại các điểm M, N sao cho
M
N
2
2
. A. (P): x - y + 2z + 2 0 B. (P): x - y + 2z 0 C. (P): x - y + 2z ± 2 0 D. (P): x - y + 2z - 2 0
Đọc tiếp
Cho mặt phẳng (Q): x - y + 2z - 2 = 0. Viết phương trình mặt phẳng (P) song song với mặt phẳng (Q), đồng thời cắt các trục Ox, Oy lần lượt tại các điểm M, N sao cho M N = 2 2 .
A. (P): x - y + 2z + 2 = 0
B. (P): x - y + 2z = 0
C. (P): x - y + 2z ± 2 = 0
D. (P): x - y + 2z - 2 = 0
Cho mặt phẳng (Q): x - y + 2z - 2 0. Viết phương trình mặt phẳng (P) song song với mặt phẳng (Q), đồng thời cắt các trục Ox, Oy lần lượt tại các điểm M, N sao cho
M
N
2
2
Đọc tiếp
Cho mặt phẳng (Q): x - y + 2z - 2 = 0. Viết phương trình mặt phẳng (P) song song với mặt phẳng (Q), đồng thời cắt các trục Ox, Oy lần lượt tại các điểm M, N sao cho M N = 2 2
![]()
![]()
![]()
![]()