tính đạo hàm của hàm số
y=\(x.e^x.lnx\)
Những câu hỏi liên quan
Tính đạo hàm các hàm số
y\(=\) \(\left(2x-1\right)\sqrt{x+1}\)
\(y'=2\sqrt{x+1}+\dfrac{2x-1}{2\sqrt{x+1}}=\dfrac{6x+3}{2\sqrt{x+1}}\)
Đúng 1
Bình luận (0)
Cho hàm sốy f(x) có đạo hàm
f
x
x
2
x
−
1
x
−
4
2
. Khi đó số điểm cực trị của hàm số
y
f
x
2
là A. 3 B. 4 C. 5 D. 2
Đọc tiếp
Cho hàm sốy = f(x) có đạo hàm f ' x = x 2 x − 1 x − 4 2 . Khi đó số điểm cực trị của hàm số y = f x 2 là
A. 3
B. 4
C. 5
D. 2
Cho hàm số f(x) có bảng xét dấu đạo hàm như hình vẽ sau Hỏi hàm số
g
x
f
1
-
x
+
x
.
e
-
x
đồng biến trên khoảng nào?
Đọc tiếp
Cho hàm số f(x) có bảng xét dấu đạo hàm như hình vẽ sau
Hỏi hàm số g x = f 1 - x + x . e - x đồng biến trên khoảng nào?
Cho hàm sốyf(x) có đạo hàm f(x) trên tập số thực
ℝ
và đồ thị của hàm số yf(x) như hình vẽ. Khi đó, đồ thị của hàm số
y
(
f
(
x
)
)
2
có A. 2 điểm cực đại, 2 điểm cực tiểu B. 2 điểm cực tiểu, 3 điểm cực đại C. 1 điểm cực đại, 3 điểm cực tiểu D. 2 điểm cực đại, 3 điểm cực tiểu
Đọc tiếp
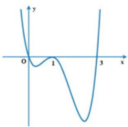
Cho hàm sốy=f(x) có đạo hàm f'(x) trên tập số thực ℝ và đồ thị của hàm số y=f(x) như hình vẽ. Khi đó, đồ thị của hàm số y = ( f ( x ) ) 2 có
A. 2 điểm cực đại, 2 điểm cực tiểu
B. 2 điểm cực tiểu, 3 điểm cực đại
C. 1 điểm cực đại, 3 điểm cực tiểu
D. 2 điểm cực đại, 3 điểm cực tiểu
Từ đồ thị hàm số f(x) ta thấy đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ x=0;x=1;x=3
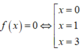
Lại thấy đồ thị hàm số y=f(x) có ba điểm cực trị nên
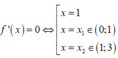
Hàm số y = f x 2 có đạo hàm y'=2f(x).f '(x)
Xét phương trình
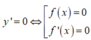
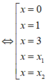
Ta có BXD của y' như sau
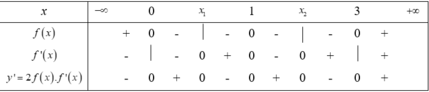
Nhận thấy hàm số y = f x 2 có y' đổi dấu từ âm sang dương tại ba điểm x=0;x=1;x=3 nên hàm số có ba điểm cực tiểu. Và y' đổi dấu từ dương sang âm tại hai điểm x = x 1 ; x = x 2 nên hàm số có hai điểm cực đại.
Chọn đáp án D.
Đúng 0
Bình luận (0)
Họ các nguyên hàm F(x) của hàm số f(x) x.lnx trên khoảng
0
;
+
∞
là
Đọc tiếp
Họ các nguyên hàm F(x) của hàm số f(x) = x.lnx trên khoảng 0 ; + ∞ là
Câu1: tính nguyên hàm của các hàm số sau
a)f(x)=x^2-3x+1/x
b)g(x)=x.e^2x
Xem chi tiết
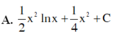
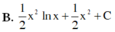
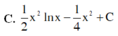
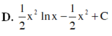
a/ \(\int\dfrac{x^2-3x+1}{x}dx=\int\left(x-3+\dfrac{1}{x}\right)dx=\int x.dx-3x+\int\dfrac{dx}{x}=\dfrac{1}{2}.x^2-3x+ln\left|x\right|+C\)
b/ \(I=\int x.e^{2x}dx\)
\(\left\{{}\begin{matrix}u=x\\dv=e^{2x}dx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=dx\\v=\dfrac{1}{2}e^{2x}\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{2}.x.e^{2x}-\dfrac{1}{2}\int e^{2x}.dx=\dfrac{1}{2}x.e^{2x}-\dfrac{1}{4}e^{2x}\)
Đúng 2
Bình luận (0)
Hồ các nguyên hàm của f(x)=x.lnx
Cho hàm số
f
(
x
)
x
.
ln
x
. Tính
P
f
(
x
)
-
x
f
(
x
)
+
x
Đọc tiếp
Cho hàm số f ( x ) = x . ln x . Tính P = f ( x ) - x f ' ( x ) + x
xét tính chẵn lẽ của hàm số
y=\(tan^72x.sin5x\)
`y=f(x)=tan^7 2x .sin5x`
`f(-x)=[tan (-2x)]^7 . sin(-5x)`
`= -tan^7 2x . (-sin5x) = tan^7 2x .sin5x = f(x)`
`=>` Chẵn.
Đúng 2
Bình luận (0)