Các câu hỏi tương tự
Họ các nguyên hàm F(x) của hàm số f(x) x.lnx trên khoảng
0
;
+
∞
là
Đọc tiếp
Họ các nguyên hàm F(x) của hàm số f(x) = x.lnx trên khoảng 0 ; + ∞ là
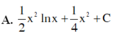
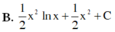
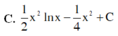
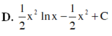
Cho hàm số
f
(
x
)
x
.
ln
x
. Tính
P
f
(
x
)
-
x
f
(
x
)
+
x
Đọc tiếp
Cho hàm số f ( x ) = x . ln x . Tính P = f ( x ) - x f ' ( x ) + x
![]()
![]()
![]()
![]()
Cho hàm số f(x) thỏa mãn f(x) + 2x f(x)
2
xe
-
x
2
và f(0)1. Tất cả các nguyên hàm của
x
f
x
e
x
2
là A. . B. . C. . D. .
Đọc tiếp
Cho hàm số f(x) thỏa mãn f'(x) + 2x f(x) = 2 xe - x 2 và f(0)=1. Tất cả các nguyên hàm của x f x e x 2 là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Giả sử F(x) là nguyên hàm của hàm số f(x)4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
Đọc tiếp
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
![]()
![]()
![]()
![]()
Họ các nguyên hàm của hàm số
f
(
x
)
1
sin
2
(
x
+
2
)
là
Đọc tiếp
Họ các nguyên hàm của hàm số f ( x ) = 1 sin 2 ( x + 2 ) là
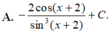
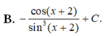
![]()
![]()
Tìm nguyên hàm của các hàm số
f
(
x
)
x
3
-
2
x
+
5
thoả mãn
F
(
1
)
3
Đọc tiếp
Tìm nguyên hàm của các hàm số f ( x ) = x 3 - 2 x + 5 thoả mãn F ( 1 ) = 3
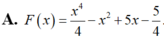
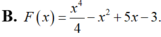
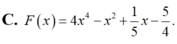
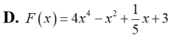
Cho F(x)
1
2
x
2
là 1 nguyên hàm của hàm số
f
(
x
)
x
. Tìm nguyên hàm của hàm số f(x)lnx
Đọc tiếp
Cho F(x) = 1 2 x 2 là 1 nguyên hàm của hàm số f ( x ) x . Tìm nguyên hàm của hàm số f'(x)lnx
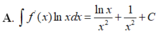
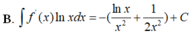
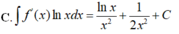
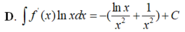
Cho
F
(
x
)
-
1
3
x
3
là một nguyên hàm của hàm số
f
(
x
)
x
Tìm nguyên hàm của hàm số f(x)lnx
Đọc tiếp
Cho F ( x ) = - 1 3 x 3 là một nguyên hàm của hàm số f ( x ) x Tìm nguyên hàm của hàm số f'(x)lnx
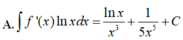
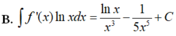
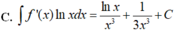
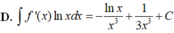
Họ các nguyên hàm của hàm số
f
(
x
)
x
e
x
2
là
Đọc tiếp
Họ các nguyên hàm của hàm số f ( x ) = x e x 2 là
![]()
![]()
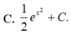
![]()





