Cho tam giác ABC có AB = AC, góc BAC=90 độ. Biết rằng M(1;-1) là trung điểm của cạnh BC và \(G\left(\frac{2}{3};0\right)\) là trọng tâm của tam giác.
Hãy tìm tọa độ các đỉnh tam giác ABC ?
5.Cho tam giác ABC với AB = AC và góc BAC = 90 độ. Đường cao BD của tam giác
ABC chia đoạn AC thành hai phần bằng nhau. Gọi M là trung điểm của AB. Chứng
minh rằng tam giác ABD và tam giác BMC bằng nhau.
Nếu theo đề này thì D trùng với A rồi bạn
c3
Cho Tam Giác ABC có Góc BAC = 60 độ và góc ABC =90 độ. tia phân giác góc BAC Cắt cạnh cắt cạnh BC tại D,từ D kẻ DE vuông góc với Ac(E Thuộc AC)
a)chứng minh Tam Giác ABD=AED
b) Chứng minh : EA=EC
c)Chứng Minh:DB<DC
d) Biết AC=2cm. tính AB;BC
a) Xét ΔABD vuông tại B và ΔAED vuông tại E có
AD chung
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
Do đó: ΔABD=ΔAED(cạnh huyền-góc nhọn)
b) Ta có: AD là tia phân giác của \(\widehat{BAC}\)(gt)
nên \(\widehat{DAC}=\dfrac{\widehat{BAC}}{2}=\dfrac{60^0}{2}=30^0\)(1)
Ta có: ΔABC vuông tại B(gt)
nên \(\widehat{C}+\widehat{A}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{DCA}+60^0=90^0\)
hay \(\widehat{DCA}=30^0\)(2)
Từ (1) và (2) suy ra \(\widehat{DAC}=\widehat{DCA}\)
Xét ΔDCA có \(\widehat{DAC}=\widehat{DCA}\)(cmt)
nên ΔDCA cân tại D(Định lí đảo của tam giác cân)
Suy ra: DA=DC(hai cạnh bên)
Xét ΔAED vuông tại E và ΔCED vuông tại E có
DA=DC(cmt)
DE chung
Do đó: ΔAED=ΔCED(cạnh huyền-cạnh góc vuông)
Suy ra: EA=EC(hai cạnh tương ứng)
c) Ta có: ΔABD=ΔAED(cmt)
nên BD=ED(Hai cạnh tương ứng)
mà ED<DC(ΔDEC vuông tại E có DC là cạnh huyền nên DC là cạnh lớn nhất)
nên DB<DC(Đpcm)
Cho tam giác ABC có góc BAC = 90 độ , AB < AC . Lấy K thuộc BC sao cho AB = BK . Gọi H là trung điểm của Ak , kéo dài BH cắt A tại J .
a, Biết góc ABC = 60 độ . Tính góc ACB
b, Chứng minh tam giác ABH = tam giác KBH , AK vuông góc BJ
c, d qua k , d // AC , d cắt AB tại D , d cắt BH tại N . Chứng minh KA là phân giác của góc JKD
Vẽ hình và giải giúp mình với ạ , mình đang cần gấp
cho tam giác ABC có góc BAC>90 độ . Kẻ AH vuông góc BC tại H. Biết AB=15 cm, AC=41 cm, BH=12 cm . Tính độ dài cạnh HC
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH vuông tại H ta có:
AB2= BH2 + AH2
<=> 152= 122+ AH2
<=> AH2= 152- 122= 225- 144= 81
<=> AH= 9 (cm)
Tương tự ta có : Áp dụng định lý Pi-ta-go vào tam giác vuông ACH vuông tại H .
AC2= AH2+ HC2
<=> 412= 92+ HC2
<=> HC2= 412- 92= 1681- 81= 1600
<=>HC= 40 (cm)
cho tam giác ABC có góc A= 90 độ. Vẽ AD ⊥ AB và AD=AB. Vẽ AE ⊥ AC và AE=AC. Biết DE=BC. Tính tam giác BAC
1.Cho tam giác ABC có góc A =120 độ.Kẻ Ax là tia phân giác góc A.Trên tia Ax lấy điểm E sao cho AE=AB+AC.Lấy điểm D sao cho AD=AB
Chứng minh rằng;
a,tam giác ABC =tam giác DBE
b,tam giác BCE là tam giác đều
2.Cho tam giác ABC nhọn có AB<AC,góc BAC < 90 độ.Đường trung trực của BC cắt tia phân giác của góc BAC tại I.Kẻ ID vuông góc với AB tại D,kẻ IE vuông góc với AC tại E
Chứng minh rằng :
tam giác EFC=tam giác ECI
Cho tam giác ABC ( góc BAC=90 độ , AB<AC ) tia phân giác của góc BAC cắt tại D . Đường thẳng vuông góc với BC tại D cắt AC tại M và cắt tia đối của tia AB tại N
a) cm tam giác ABC đồng dạng với tam giác DBN và BA.BN=BD.BC
b) cm DB=Dm
mọi người giúp em giải với
xét ΔABC và ΔDBN ta có
\(\widehat{B}\) chung
\(\widehat{BAC}=\widehat{BDN}=90^o\)
=>ΔABC∼ΔDBN(g.g)
=>\(\dfrac{BA}{BD}=\dfrac{BC}{BN}\)
=>\(BA.BN=BD.BC\)
Cho tam giác ABC có góc b, góc c nhọn.AH là đường cao AM là trung tuyến ,biết rằng góc bah =góc mac . BE là trung điểm ab: a)C/m a,m,h,e cùng thuộc một đường tròn
b) C/M góc BAC=90 độ
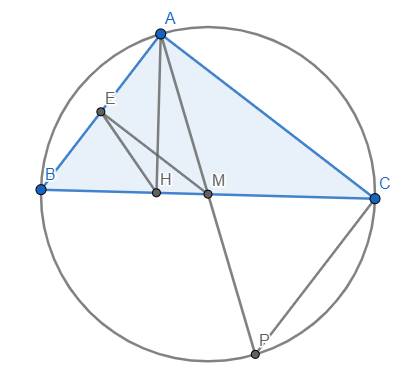
a) Gọi P là giao điểm của AM với (O). Tam giác ABH và APC có:
\(\widehat{BAH}=\widehat{PAC}\left(gt\right)\) và \(\widehat{ABH}=\widehat{APC}\) (góc nội tiếp cùng chắn cung AC)
\(\Rightarrow\Delta ABH~\Delta APC\left(g.g\right)\) \(\Rightarrow\widehat{AHB}=\widehat{ACP}\).
Mà \(\widehat{AHB}=90^o\Rightarrow\widehat{ACP}=90^o\) . Suy ra M nằm trên đường kính AP của (O).
Mặt khác, M lại là trung điểm của dây BC của (O), do đó nếu dây BC không phải là đường kính của (O) thì phải có \(AP\perp BC\) , điều này không chắc chắn đúng. Do đó để đảm bảo M là trung điểm BC thì BC phải là đường kính của (O).
\(\Rightarrow\) M là tâm của (O). Từ đó \(\widehat{MBA}=\widehat{MAB}\)
Trong tam giác HAB vuông tại H có trung tuyến HE nên \(EH=EA=EB=\dfrac{AB}{2}\), do đó \(\widehat{ABM}=\widehat{EHB}\).
Từ đó suy ra \(\widehat{MAB}=\widehat{EHB}\) \(\Rightarrow\) Tứ giác AMHE nội tiếp (đpcm)
b) Từ câu a), ta có BC là đường kính của (O) nên suy ra đpcm.
CHO TAM GIÁC ABC VẼ PHÂN GIÁC AD,DE,BC QUA D KẺ DM SONG SONG AB,M THUỘC AC,QUA M KẺ MK SONG SONG AD ,CHỨNG MINH RẰNG MK LÀ PHÂN GIÁC CỦA GÓC DMC
NẾU CHO GÓC BAC =90 ĐỘ ,CHỨNG MINH DM VUÔNG GÓC AC VÀ TÍNH SỐ ĐO CỦA GÓC KMC