Câu1:hình thang cân ABCD(AB//CD; AB< CD)Ta có:
A. AB=CD B. AC//BD
C.A^ =B^;C^=D^ D. AD//BC
câu 2: cho hình bình hành ABCD có C^ = 80o khi đó A^ là:
a. 100o b.80o c.40o d.90o
Xem thêm câu trả lời
Chiếu một tia sáng lên một gương phẳng ta thu được một tia phản xạ tạo với tia tới một góc 80o. Góc tới có giá trị nào sau đây ?
A.20o B.40o C.60o D.80o
Giúp với
Xem thêm câu trả lời
Cho tam giác MNP có \(\widehat{M}\) = 25o. \(\widehat{N}\) = 80o thì góc ngoài của tam giác tại đỉnh P có số đo bằng?
Chiếu một tia sáng lên một gương phẳng ta thu được một tia phản xạ tạo với tia tới một góc 40o. Góc tới có giá trị nào sau đây?
A. 20o
B. 80o
C. 40o
D. 60o
Đáp án: A
Ta có tia phản xạ tạo với tia tới một góc 40o, mà góc phản xạ và góc tới bằng nhau nên giá trị của góc tới là: 40 : 2 = 20o
Đúng 0
Bình luận (0)
Tam giác ABC có
∠
A
80
o
,
∠
B
40
o
.
Các đường phân giác BD, CE cắt nhau tại I. Khi đó số đo góc (ACI) là: A.
100
o
B.
80
o
C.
60
o
D.
30
o
Đọc tiếp
Tam giác ABC có ∠ A = 80 o , ∠ B = 40 o . Các đường phân giác BD, CE cắt nhau tại I. Khi đó số đo góc (ACI) là:
A. 100 o
B. 80 o
C. 60 o
D. 30 o
Ta có ∠C = 180o - 80o - 40o = 60o
Vì CI là tia phân giác của góc C nên ∠(ACI) = 60o : 2 = 30o. Chọn D
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có hat{A} 100o, widehat{B} 100o, widehat{D} 80o. Lấy E,F lần lượt là trung điểm của AD, BC. O là giao điểm của AC và BD.a) CMR: ABCD là hình thang cân và tính góc C.b) Cho AB 20 cm, CD 30cm. Tính EF, EO, FO.c) CMR: DeltaABC DeltaABD, DeltaACD DeltaBDC, DeltaAEO DeltaBFO.d) Giả sử AD 20cm. Tính BC, góc ABD, góc ADB, góc AOD, góc AOB.
Đọc tiếp
Cho tứ giác ABCD có \(\hat{A}\)= 100o, \(\widehat{B}\)= 100o, \(\widehat{D}\)= 80o. Lấy E,F lần lượt là trung điểm của AD, BC. O là giao điểm của AC và BD.
a) CMR: ABCD là hình thang cân và tính góc C.
b) Cho AB = 20 cm, CD = 30cm. Tính EF, EO, FO.
c) CMR: \(\Delta\)ABC = \(\Delta\)ABD, \(\Delta\)ACD = \(\Delta\)BDC, \(\Delta\)AEO = \(\Delta\)BFO.
d) Giả sử AD = 20cm. Tính BC, góc ABD, góc ADB, góc AOD, góc AOB.
Cho hình thang ABCD có AD// BC và
∠
B
A
D
100
o
;
∠
A
D
C
80
o
. Tìm khẳng định sai A. AB CD; AD BC B. Tứ giác ABCD là hình bình hành C.
B
A
D
^
B
C
D
^...
Đọc tiếp
Cho hình thang ABCD có AD// BC và ∠ B A D = 100 o ; ∠ A D C = 80 o . Tìm khẳng định sai
A. AB = CD; AD = BC
B. Tứ giác ABCD là hình bình hành
C. B A D ^ = B C D ^ = 100 ° , A B C ^ = A D C ^ = 80 °
D. AC = BD
* Ta có: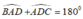 
Và 2 góc này ở vị trí trong cùng phía nên AB// CD (1)
* Lại có: AD// BC ( giả thiết) (2)
Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành (dấu hiệu nhận biết).
* Suy ra: AB = CD; AD = BC;
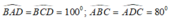
Chọn đáp án D
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B= 80o, C=40o. tia phân giác của góc B cắt cạnh AC tại D. Kẻ tia DE song song với BC ( E nằm giữa A và B)
Tính góc A
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Tính ∠(BIC) biết rằng: ∠B = 80o,∠C = 40o
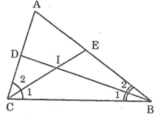
∠B = 80o, ∠C = 40o
Ta có:
∠(B1) = (1/2)∠(ABC) = (1/2).80o = 40o (vì BD là tia phân giác ∠(ABC))
∠(C1) = (1/2)∠(ACB) = (1/2).40o = 20o (vì CE là tia phân giác ∠(ACB))
Trong ΔIBC, ta có: ∠(BIC) + ∠(B1) + ∠(C1) = 180o(tổng 3 góc trong tam giác)
Vậy: ∠(BIC) = 180o - (∠(B1) + ∠(C1)) = 180o - (40o + 20o) = 120o
Đúng 0
Bình luận (0)
Viết tiếp vào chỗ chám cho thích hợp
Cho hình bình hành MNPQ cóđáy QP bằng 5 xăng ti mét và chiều cao MH bằng 3 cm
Diện tích hình tam giác MQP là
Diện tích hình tam giác MNP là