Trong các hàm sau đây, hàm nào là hàm riêng của toán tử d/dx2. Tìm trị riêng ứng với hàm riêng đó?
a) sinkx
b) coskx
c) exp(kx)
d) sinkx + coskx
Hàm nào là hàm riêng của d2/d(x2)
a) k
b) kx
Đạo hàm cấp 2 của k và kx theo x đều là hằng số nên cả 2 ý đều không phải là hàm riêng của d2/d(x2)
@Tuấn Anh
Sách bảo có là hàm riêng ông ạ :3
Chứng minh rằng hàm số cos(ax).cos(by).cos(cz) là hàm riêng của toán tử Laplace (\(\nabla\)2).
(d/dx2+d/dy2+d/dz2)(cos(ax).cos(by).cos(cz))
= d/dx2(cos(ax).cos(by).cos(cz))+d/dy2(cos(ax).cos(by).cos(cz))+d/dz2(cos(ax).cos(by).cos(cz))
= -a2.cos(ax).cos(by).cos(cz) - b2.cos(ax).cos(by).cos(cz) - c2.cos(ax).cos(by).cos(cz)
= ( -a2 - b2 - c2).cos(ax).cos(by).cos(cz)
vậy hàm số trên là hàm riêng của toán tử Laplace và có trị riêng là -a2 - b2 - c2
Câu 5.
Trong các hàm số cho dưới đây, hàm nào là hàm riêng của toán tử Laplace. Trong trường hợp nếu là hàm riêng thì hãy chỉ ra trị riêng của nó?
a) sin(x + y + z)
b) cos(xy+yz+zx)
c) exp(x2 + y2 + z2)
d) ln(xyz)
phương trình dạng toán tử : \(\widehat{H}\)\(\Psi\) = E\(\Psi\)
Toán tử Laplace: \(\bigtriangledown\)2 = \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\)
thay vào từng bài cụ thể ta có :
a.sin(x+y+z)
\(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))sin(x+y+z)
=\(\frac{\partial^2}{\partial x^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial y^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial z^2}\)sin(x+y+z)
=\(\frac{\partial}{\partial x}\)cos(x+y+z) + \(\frac{\partial}{\partial y}\)cos(x+y+z) + \(\frac{\partial}{\partial z}\)cos(x+y+z)
= -3.sin(x+y+z)
\(\Rightarrow\) sin(x+y+z) là hàm riêng. với trị riêng bằng -3.
b.cos(xy+yz+zx)
\(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))cos(xy+yz+zx)
=\(\frac{\partial^2}{\partial x^2}\)cos(xy+yz+zx) +\(\frac{\partial^2}{\partial y^2}\)cos(xy+yz+zx) + \(\frac{\partial^2}{\partial z^2}\)cos(xy+yz+zx)
=\(\frac{\partial}{\partial x}\)(y+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial y}\)(x+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial z}\)(y+x).-sin(xy+yz+zx)
=- ((y+z)2cos(xy+yz+zx) + (x+z)2cos(xy+yz+zx) + (y+x)2cos(xy+yz+zx))
=-((y+z)2+ (x+z)2 + (x+z)2).cos(xy+yz+zx)
\(\Rightarrow\) cos(xy+yz+zx) không là hàm riêng của toán tử laplace.
c.exp(x2+y2+z2)
\(\bigtriangledown\)2 f(x,y,z) = (\(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+ \(\frac{\partial^2}{\partial z^2}\))exp(x2+y2+z2) =\(\frac{\partial^2}{\partial x^2}\)exp(x2+y2+z2)+\(\frac{\partial^2}{\partial y^2}\)exp(x2+y2+z2) +\(\frac{\partial^2}{\partial z^2}\)exp(x2+y2+z2) =\(\frac{\partial}{\partial x}\)2x.exp(x2+y2+z2)+\(\frac{\partial}{\partial y}\)2y.exp(x2+y2+z2)+\(\frac{\partial}{\partial z}\)2z.exp(x2+y2+z2) =2.exp(x2+y2+z2) +4x2.exp(x2+y2+z2)+2.exp(x2+y2+z2) +4y2.exp(x2+y2+z2)+2.exp(x2+y2+z2) +4z2.exp(x2+y2+z2) =(6+4x2+4y2+4z2).exp(x2+y2+z2)\(\Rightarrow\)exp(x2+y2+z2) không là hàm riêng của hàm laplace.d.ln(xyz)\(\bigtriangledown\)2 f(x,y,z) = (\(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+ \(\frac{\partial^2}{\partial z^2}\))ln(xyz) =\(\frac{\partial^2}{\partial x^2}\)ln(xyz)+\(\frac{\partial^2}{\partial y^2}\)ln(xyz)+\(\frac{\partial^2}{\partial z^2}\)ln(x+y+z) =\(\frac{\partial}{\partial x}\)yz.\(\frac{1}{xyz}\) + \(\frac{\partial}{\partial y}\)xz.\(\frac{1}{xyz}\) + \(\frac{\partial}{\partial z}\)xy.\(\frac{1}{xyz}\) =\(\frac{\partial}{\partial x}\)\(\frac{1}{x}\) + \(\frac{\partial}{\partial y}\)\(\frac{1}{y}\)+\(\frac{\partial}{\partial z}\)\(\frac{1}{z}\) = - \(\frac{1}{x^2}\)- \(\frac{1}{y^2}\)- \(\frac{1}{z^2}\)\(\Rightarrow\) ln(xyz) không là hàm riêng của hàm laplace.Bạn Hồng gửi lại đáp án, bạn gõ trực tiếp câu trả lời lên web, không gửi dưới dạng ảnh.
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.
Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D
Cho hàm số f x = a x 5 + b x 4 + c x 3 + d x 2 + e x + f với a, b, c, d, e, f là các số thực; đồ thị của y = f ' x như hình vẽ bên. Hàm số y = f 1 - 2 x - 2 x 2 + 1 đồng biến trên khoảng nào dưới đây?
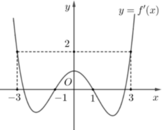
A. - 3 2 ; - 1
B. - 1 2 ; 1 2
C. (-1;0)
D. (1;3)
Chọn đáp án C.
Ta có
![]()
![]()
Đặt t = 1 - 2 x bất phương trình trở thành f ' t < t - 1
kẻ thêm đường thẳng y = x - 1 qua hai điểm (1;0);(3;2) trên đồ thị
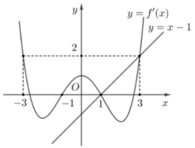
Ta có f ' t < t - 1
![]()
Đối chiếu các đáp án chọn C
Với điều kiện nào của m thì các hàm số dưới đây là hàm số bậc nhất?
a) y = (m-1)x + m
b) y = (m2-2x -3)x2 + (m+1)x + m
c) y = √(m2-1).x + 2 .
@ hoàng thị thanh hoa
xin phép tag bn hoa vào đây đọc đc thì nhắn tin riêng vs mik
a: ĐKXĐ: m<>1
b: ĐKXĐ: \(m^2-2m-3-m-1< >0\)
=>(m-4)(m+1)<>0
hay \(m\notin\left\{4;-1\right\}\)
Đường cong trong hình bên là đồ thị của một hàm số trong các hàm số ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
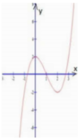
A. y = x 3 - 3 x 2 + 2
B. y = x 3 + 3 x + 1
C. y = - x 3 + 3 x 2 + 2
D. y = x 4 - 3 x 2 + 2
Đường cong trong hình bên là đồ thị của một hàm số trong các hàm số ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
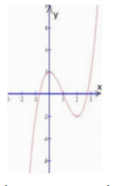
A. y = x 3 - 3 x 2 + 2
B. y = x 3 + 3 x + 1
C. y = - x 3 - 3 x 2 + 2
D. y = x 4 - 3 x 2 + 2
Chọn A.
Đồ thị không phải là của hàm số bậc 4 nên loại D.
Đồ thị là của hàm số bậc 3 có hệ số a > 0 nên loại C.
Đồ thị hàm số có 2 điểm cực trị nên đạo hàm có 2 nghiệm phân biệt
Xét đạo hàm: A. ![]() có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
1. Điểm nào dưới đây thuộc đồ thị hàm số y =-5x+3?
A. M(2;13) B.N(2;-7) C.P(-2;-7) DQ (1;8)
2. Hàm số nào dưới đây là hàm số bậc nhất?
A. y=7 B.y=0x+5 C. y=3x^2-1 D. y=1/2x-4
Bài1: Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Tìm hệ số a,b của hàm số bậc nhất đó?
a/ y=3x-2 b/3x^2-1 c/y=0x+5 d/y=-2.(x+5)- e/y=1+x/2
Câu 1: B
Câu 2: D
Bài 1: Các hàm số bậc nhất là
a: y=3x-2
a=3; b=-2
d: y=-2(x+5)
=-2x-10
a=-2; b=-10
e: \(y=1+\dfrac{x}{2}\)
\(a=\dfrac{1}{2};b=1\)