Tìm đk:

Những câu hỏi liên quan
Bài 1: Cho phương trình: (m-1)x+1=0 (1)
a) Tìm ĐK của m để pt (1) là pt bậc nhất một ẩn.
b) Tìm ĐK của m để pt (1) có nghiệm x = -5.
c) Tìm ĐK của m để pt (1) vô nghiệm.
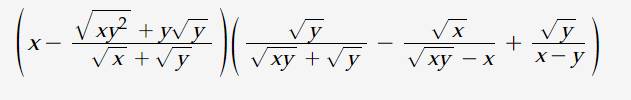
Tìm đk và rút gọn
ĐKXĐ: x>0 và y>0
Sửa đề: \(A=\left(x-\dfrac{\sqrt{xy^2}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}\right)\left(\dfrac{\sqrt{y}}{\sqrt{xy}+y}-\dfrac{\sqrt{x}}{\sqrt{xy}-x}+\dfrac{\sqrt{y}}{x-y}\right)\)
\(=\left(x-\dfrac{y\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}\right)\left(\dfrac{\sqrt{y}}{\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)}-\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{y}-\sqrt{x}\right)}+\dfrac{\sqrt{y}}{x-y}\right)\)
\(=\left(x-y\right)\cdot\left(\dfrac{1}{\sqrt{x}+\sqrt{y}}+\dfrac{1}{\sqrt{x}-\sqrt{y}}+\dfrac{\sqrt{y}}{x-y}\right)\)
\(=\left(x-y\right)\cdot\dfrac{\sqrt{x}-\sqrt{y}+\sqrt{x}+\sqrt{y}+\sqrt{y}}{x-y}\)
\(=2\sqrt{x}+\sqrt{y}\)
Đúng 2
Bình luận (0)
√ - 8 phần 3x2 + 4 ( tìm đk)
ĐKXĐ: -8/3x^2+4>=0
=>-8/3x^2>=-4
=>x^2<=4:8/3=12/8=3/2
=>-căn 3/2<=x<=căn 3/2
Đúng 1
Bình luận (0)
\(\sqrt{\dfrac{-8}{3x^2+4}}\)
Để biểu thức trên xác định thì mẫu > 0
Mà \(x^2\ge0\) => \(3x^4+4>0\)
Đúng 1
Bình luận (0)
Tìm đk rồi rút gọn câu 4
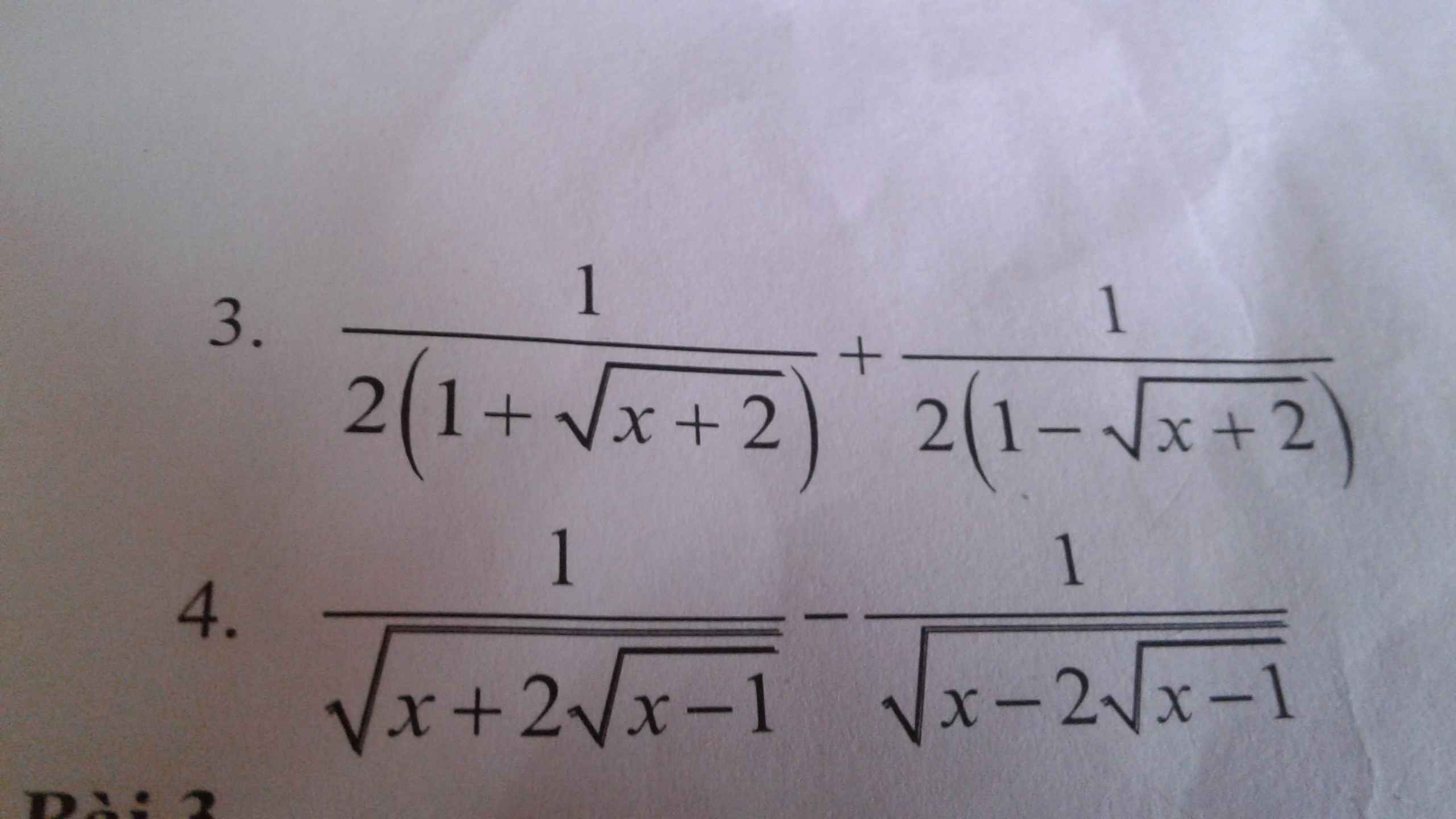
Tam thức bậc 2 ,tìm đk tham số m
Dùng bảng biến thiên, tại giờ không có điện thoại nên ko gửi được
Đúng 1
Bình luận (0)
tìm x
căn 3x + 2 > 4 (đk x > -2/3)
\(\Leftrightarrow3x+2>16\)
hay \(x>\dfrac{14}{3}\)
Đúng 0
Bình luận (0)
Tìm ĐK : A= \(\dfrac{1}{\sqrt{x-\sqrt{2x-1}}}\)
cuối cùng cx tìm đk nhau
b©y gi¬ mµy lµ kÎ thï kh«ng ®éi tr¬i chung cña t¸o
Đúng 0
Bình luận (1)
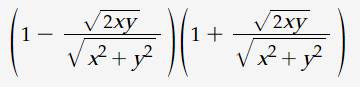
Tìm đk , rút gọn và tính P khi a = b
Sửa đề: a = b => x = y
\(P=\left(1-\dfrac{\sqrt{2xy}}{\sqrt{x^2+y^2}}\right)\left(1+\dfrac{\sqrt{2xy}}{\sqrt{x^2+y^2}}\right)\) (ĐK: \(x,y>0\))
\(=1-\left(\dfrac{\sqrt{2xy}}{\sqrt{x^2+y^2}}\right)^2\)
\(=1-\dfrac{\left(\sqrt{2xy}\right)^2}{\left(\sqrt{x^2+y^2}\right)^2}\)
\(=1-\dfrac{2xy}{x^2+y^2}\)
\(=\dfrac{x^2+y^2-2xy}{x^2+y^2}\)
\(=\dfrac{\left(x-y\right)^2}{x^2+y^2}\)
Khi x = y, ta được: \(P=\dfrac{\left(x-y\right)^2}{x^2+y^2}=\dfrac{\left(x-x\right)^2}{x^2+y^2}=0\)
#Urushi
Đúng 3
Bình luận (0)















 _<❤' onerror='this.src="/assets/img/avt/2.png"' style='width:36px;height:auto' />
_<❤' onerror='this.src="/assets/img/avt/2.png"' style='width:36px;height:auto' />


