Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat {{B_2}}\)
b) Tính số đo các góc \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo các góc \(\widehat {{B_1}},\widehat {{A_1}}\).
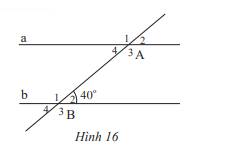
Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat {{B_2}}\)
b) Tính số đo các góc \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo các góc \(\widehat {{B_1}},\widehat {{A_1}}\).

a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)
Cho hình thang vuông ABCD (AB // CD) có \(\widehat{A}=\widehat{D}=90^0,\widehat{B}=60^0,CD=30cm,CA\perp CB\) . Tính diện tích của hình thang ABCD.
Cho hình chóp S.ABC, có \(\widehat{ASB\:=}90^0,\widehat{BSC}=60^0,\widehat{CSA}=120^0.\) Tính khoảng cách từ C đến (SAB).
A. \(\dfrac{a}{4}\)
B. a
C. \(\dfrac{a}{2}\)
D. \(\dfrac{3a}{2}\)
Cho hình vẽ sau: https://scontent.fsgn5-1.fna.fbcdn.net/v/t1.15752-9/72553220_465790920811870_6590605608947286016_n.png?_nc_cat=101&_nc_oc=AQnWU6dSKl8dKnXKRDuhswJmAQA1PCZs9SE2i0ypFOssa5Rt1nzPbp_EYQGgczI2ama5fhA0RehHV7KtO8IzW6YD&_nc_ht=scontent.fsgn5-1.fna&oh=ccd9a35086c6676d218d3a9a3dbe1da0&oe=5E2AAA7B
biết a//b và \(\widehat{A_2}=80^0\)
a) tìm cặp góc sole trong bằng nhau
b) Tìm các cặp góc đông vị bằng nhau
c) Tính \(\widehat{A_3};\widehat{A_4};\widehat{B_1};\widehat{B_2}\)
Cho hình chóp S.ABC, có \(\widehat{ASB\: =}90^0,\widehat{BSC}=60^0,\widehat{CSA}=120^0,SC=a\sqrt{2}.\) Tính khoảng cách từ C đến (SAB).
A. \(\dfrac{a}{4}\)
B. a
C. \(\dfrac{a}{2}\)
D. \(\dfrac{3a}{2}\)
Đặt \(SA=x;SB=y\)
\(S_{\Delta SAB}=\dfrac{1}{2}SA.SB=\dfrac{xy}{2}\)
\(V=\dfrac{SA.SB.SC}{6}.\sqrt{1+2.cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{axy}{6}\)
\(\Rightarrow d\left(C;\left(SAB\right)\right)=\dfrac{3V}{S}=\dfrac{axy}{2.\dfrac{xy}{2}}=a\)
Cho hình 1 . Biết a//b, \(\widehat{A_4}=42^0\)
a) Hãy nêu tên một cặp góc so le trong và một cặp góc đồng vị.
b) Tính \(\widehat{B_1},\widehat{B_2}\)
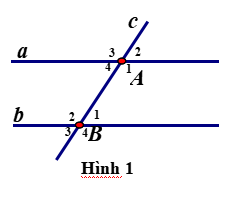
Các bạn giúp mik với!! ai xong mik tick cho!!
\(a,\text{So le trong: }\widehat{A_1}\text{ và }\widehat{B_2}\\ \text{Đồng vị: }\widehat{A_1}\text{ và }\widehat{B_4}\\ b,a\text{//}b\Rightarrow\widehat{A_1}=\widehat{B_2}=42^0\\ \Rightarrow\widehat{B_1}=180^0-\widehat{B_2}=138^0\left(\text{kề bù}\right)\)
Cho hình chóp S.ABC, có \(\widehat{ASB\: =}90^0,\widehat{BSC}=60^0,\widehat{CSA}=120^0,SA=a,SB=a\sqrt{3},SC=a\sqrt{2}.\) Tính thể tích khối chóp S.ABC
A. \(\dfrac{a^2\sqrt{3}}{6}\)
B. \(\dfrac{a^2\sqrt{3}}{2}\)
C. \(\dfrac{a^2\sqrt{2}}{6}\)
D. \(\dfrac{a^2\sqrt{3}}{4}\)
\(V=\dfrac{a.a\sqrt{3}.a\sqrt{2}}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290-cos^260-cos^2120}=\dfrac{a^3\sqrt{3}}{6}\)
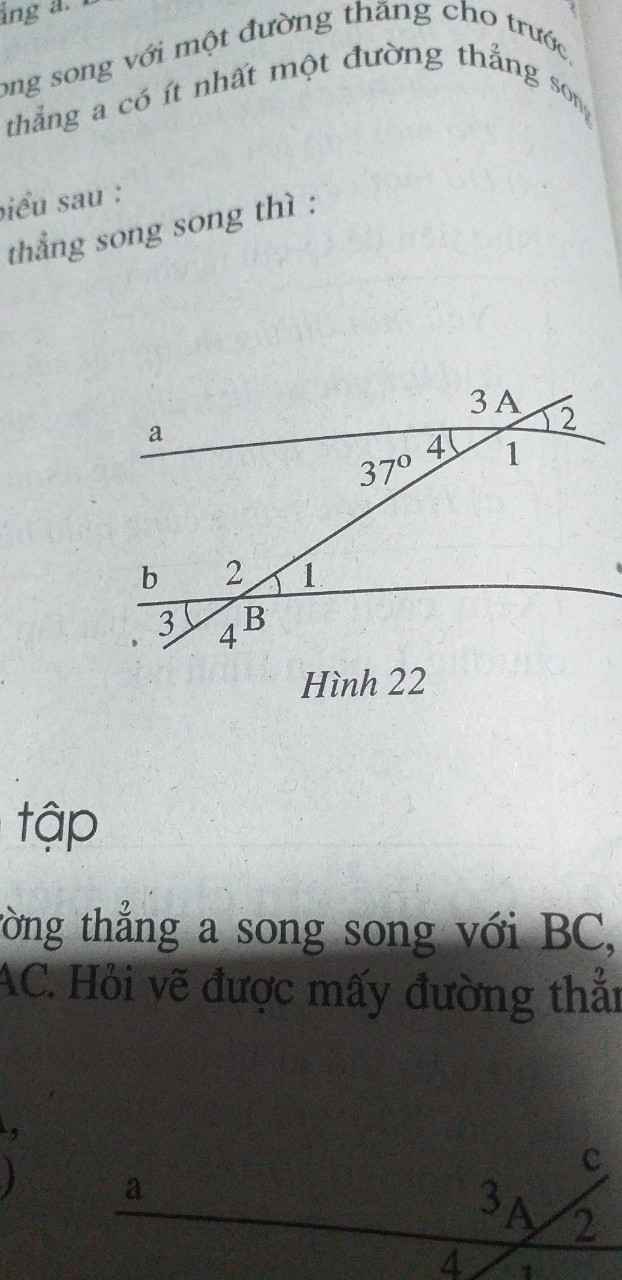
Hình 22 cho biết a // b và \(\widehat{A}_4\) = \(37^o\) .
a) Tính \(\widehat{B_1}\) .
b) So sánh \(\widehat{A_1}\) và \(\widehat{B_4}\) .
c) Tính \(\widehat{B_2}\)
Cho 2 đường thẳng a và b.Đường thẳng AB cắt hai đường thẳng trên tại A và B/
a.Nếu biết \(\widehat{A_1}=120^o\);\(\widehat{B_3=130^o}\)thì hai đường thẳng a và b có song song với nhau hay k?Muốn a//với b thì phải đổi thế nào?
b.Biết \(\widehat{A_2}=65^o\);\(\widehat{B_2}\)=\(64^o\)thì a và b có song song không .Muốn a//b thì phải đổi như thế nào?
Cho tứ diện ABCD, có \(\widehat{BAC}=90^0,\widehat{CAD}=60^0,\widehat{BAD}=120^0;AB=AC=AD=a\). Tính khoảng cách từ B đến (ACD).
A. \(\dfrac{a\sqrt{6}}{3}\)
B. \(\dfrac{a\sqrt{3}}{2}\)
C. \(\dfrac{a\sqrt{6}}{2}\)
D. \(\dfrac{a\sqrt{3}}{4}\)