hình trên cho biết a // b và A4 370 a) tính B1b ) so sánh A1 và B4c) tính B2abA1234B2341
Đọc tiếp
hình trên cho biết a // b và A4 = 370
a) tính B1
b ) so sánh A1 và B4
c) tính B2
Những câu hỏi liên quan
6 tháng 10 2021 lúc 7:31
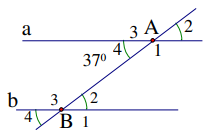
Hình 22 cho biết a // b và A4 = 37'( độ )
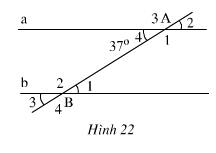
a) Tính B1
b) So sánh A1 và B4
c) Tính B2
a, a//b \(\Rightarrow\widehat{A_4}=\widehat{B_1}=37^0\left(so.le.trong\right)\)
b, a//b \(\Rightarrow\widehat{A_1}=\widehat{B_4}\left(đồng.vị\right)\)
c, \(\widehat{B_2}+\widehat{B_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{B_2}=180^0-37^0=143^0\)
Đúng 2
Bình luận (1)
a) Ta có: a//b
⇒A4=B1=370(so le trong)
b) Ta thấy a//b
A1 và B4 là 2 góc đồng vị
⇒A1=B4
c) Ta lại có: A4+B2=1800(trong cùng phía)
⇒370+B2=1800
⇒B2=1800-370=1430
Đúng 1
Bình luận (0)
Bài 3. Cho hình 2 biết a // b và A4 = 370. a) Tính B2 . b) So sánh A1 và B1. c) Tính B3
a. \(A_4=B_2=37^0\left(slt\right)\)
b. \(A_1=B_1\left(dongvi\right)\)
c. \(B_3=180^0-B_2=180^0-37^0=143^0\left(kebu\right)\)
Đúng 1
Bình luận (1)
Cho hình vẽ sau: biết a//b và A1=54 độ
a)tính B2
b)so sánh A1 và B3
c)tính A4+B2
Do a // b nên ta có:
\(\widehat{A_1}=\widehat{A_3}=54^0(đối đỉnh)\)
\(\widehat{A_3}+\widehat{A_2}=180^0\)
\(\Rightarrow\)\(\widehat{A_2}=180^0-54^0=126^0\)
a)\(\widehat{B_2}=\widehat{A_3}=54^0(đồng vị)\)
b)\(\widehat{A_2}=\widehat{A_4}=126^0(đối đỉnh)\)
\(\Rightarrow\)\(\widehat{A_4}=\widehat{B_3}=126^0(đồng vị)\)
\(\widehat{A_1}<\widehat{B_3}(54^0<126^0)\)
c)\(\widehat{A_4}+\widehat{B_2}=126^0+54^0=180^0\)
Đúng 1
Bình luận (1)
Hình 22 cho biết a//b và A4 = 37o
So sánh góc A1 và góc B4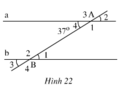
a // b nên A 1 ^ = B 4 ^ (Hai góc đồng vị)
Đúng 0
Bình luận (0)
Cho biết a//b và A4 = 37o
a) Tính góc B1
b) So sánh góc A1 và góc B4
c) Tính góc B2
A/tính góc B1
A4=A1=37 o(2 góc đối đỉnh)
A1=B1= 37o( sole trong)
B/
A1 và B4 ở vị trí trong cùng phía ( bù nhau )
=>A1+B4=180o
=>35+B4=180o
=>B4=180-35
=>B4=145o
C/
Vì B4 và B2 đối đình(bằng nhau)
=> B4=B2=145o
học tốt ><
Cho hai đường thẳng a,b song song. Đường thẳng c cắt a tại điểm A và cắt b tại B. Biết góc A1 = B3.
a) So sánh góc A4;B2
b) So sánh góc A1;B1
c) Tính góc A1+B2
hình cho biết a//b và B1 = 40 độ a) Tính A4 b) So sánh A3 và B2 C) Tính B4
Trên hình biết a // b và góc B2=40 độ:
a) Tính góc A1
b) So sánh góc A3 và B1
c) Tính góc A2+B1
\(a,a//b\Rightarrow\widehat{B_2}+\widehat{A_1}=180^0\left(trong.cùng.phía\right)\\ \Rightarrow\widehat{A_1}=180^0-40^0=140^0\\ b,a//b\Rightarrow\widehat{A_1}=\widehat{B_1}\left(đồng.vị\right)\\ Mà.\widehat{A_1}=\widehat{A_3}\left(đối.đỉnh\right)\\ \Rightarrow\widehat{A_3}=\widehat{B_1}\\ c,Ta.có.\widehat{A_2}+\widehat{B_1}=\widehat{A_2}+\widehat{A_1}=180^0\left(kề.bù\right)\)
Đúng 1
Bình luận (1)
a. Ta có: a // b
=> \(\widehat{B_2}+\widehat{A_1}=180^o\) (2 góc trong cùng phía)
Mà \(\widehat{B_2}=40^o\)
=> \(\widehat{A_1}=180^o-40^o=140^o\)
b. Ta có: \(\widehat{A_1}=\widehat{B_3}\) (so le trong) (1)
Ta lại có: \(\left\{{}\begin{matrix}\widehat{A_1}=\widehat{A_3}\left(ĐĐ\right)\\\widehat{B_1}=\widehat{B_3}\left(ĐĐ\right)\end{matrix}\right.\) (2)
Từ (1) và (2), suy ra:
\(\widehat{A_3}=\widehat{B_1}\)
c. Ta có: a // b
=> \(\widehat{A_1}=\widehat{B_1}=140^o\) (đồng vị)
\(\widehat{B_2}=\widehat{A_2}=40^o\) (đồng vị)
=> \(\widehat{A_2}+\widehat{B_1}=140^o+40^o=180^o\)
Đúng 0
Bình luận (0)
Cho hình vẽ bên biết a // b và
A
1
^
+
A
2
^
+
A
3
^
310
°
.a) Tính
A
1
^
b) So sánh
A
2
^
và ...
Đọc tiếp
Cho hình vẽ bên biết a // b và A 1 ^ + A 2 ^ + A 3 ^ = 310 ° .
a) Tính A 1 ^
b) So sánh A 2 ^ và B 4 ^
a) Ta có: A 1 ^ + A 2 ^ + A 3 ^ = 310 ° mà A 2 ^ + A 3 ^ = 180 ° ( hai góc kề bù)
do đó A 1 ^ = 310 ° − 180 ° = 130 ° .
b) Ta có: B 2 ^ = A 2 ^ (hai góc đồng vị); B 2 ^ = B 4 ^ (hai góc đối đỉnh).
Suy ra A 2 ^ = B 4 ^
Đúng 0
Bình luận (0)
Sô ươc cua 23 la mây?
Số uoc cua 23 la A1 B4 C3 D2 chon đap ap đung
Cho góc A4 = 37độ , a // b , a) tính B1 , b) so sánh A1 và B4 , c) tính B2 . Giải thích cho mình hiểu nha , cảm ơn
