Giúp e bài 7 vvới ạ 

Những câu hỏi liên quan
Giúp e bài 7 ạ
Người đó lãi:\(\left(728000:650000\right)-100\%=12\%\)
Đúng 1
Bình luận (0)
Giúp e bài 7 đi ạ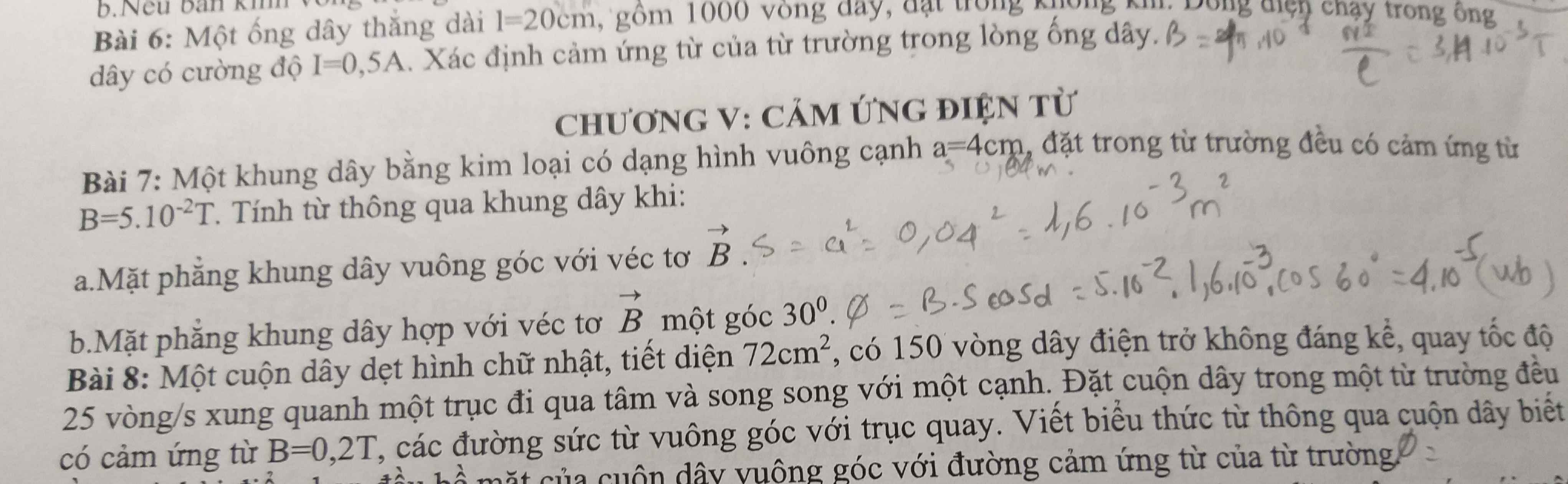
Bài 7.
a)Mặt phẳng khung dây vuông góc với vecto \(\overrightarrow{B}\)\(\Rightarrow\left(\overrightarrow{n},\overrightarrow{B}\right)=0^o\)\(\overrightarrow{B}\)\(\overrightarrow{B}\)\(\overrightarrow{B}\)
Từ thông qua khung dây:
\(\Phi=BS\cdot cos\alpha=5\cdot10^{-2}\cdot0,04^2\cdot cos0^o=8\cdot10^{-5}Wb\)
b)Mặt phẳng khung dây hợp với \(\overrightarrow{B}\) một góc \(30^o\Rightarrow\left(\overrightarrow{n};\overrightarrow{B}\right)=60^o\)
Từ thông qua khung dây:
\(\Phi=BS\cdot cos\alpha=5\cdot10^{-2}\cdot0,04^2\cdot cos60^o=4\cdot10^{-5}Wb\)
Đúng 2
Bình luận (0)
giải giúp e bài 7 với ạ;-;
Nhờ mn làm giúp e bài 7 ạ
7.
1. getting - went
2. was hoping - gave
3. was living- spent
4. started - was checking in
5. was looking - saw
6. came - was showing
7. was playing - broke
Đúng 3
Bình luận (0)
Mọi người giúp e làm và cách làm phương pháp nhóm rồi rút nhân tử chung với ạ. mn giúp e một số câu nx ạ . BÀI 7 ý mn

Mọi người giúp e câu 8 bài 7 với ạ

\(A=x^7-4x^3+x^2+2=x^3\left(x^4-4\right)+x^2+2\)
\(=x^3\left(x^2-2\right)\left(x^2+2\right)+x^2+2\)
\(=\left(x^2+2\right)\left(x^3\left(x^2-2\right)+1\right)\)
\(=\left(x^2+2\right)\left(x^5-2x^3+1\right)\)
\(=\left(x^2+2\right)\left(x^5-x^4+x^4-x^3-x^3+x^2-x^2+x-x+1\right)\)
\(=\left(x^2+2\right)\left[x^4\left(x-1\right)+x^3\left(x-1\right)-x^2\left(x-1\right)-x\left(x-1\right)-\left(x-1\right)\right]\)
\(=\left(x^2+2\right)\left(x-1\right)\left(x^4+x^3-x^2-x-1\right)\)
Đúng 0
Bình luận (0)
Có ai biết bài: Test for unit 4 English 7 k ạ?
Nếu bết thỳ giải giúp e 2 bài cuối của test vs ạ
ai đag onl giải giúp e
Giúp em bài 7 với ạ😞😞😞. E cảm ơn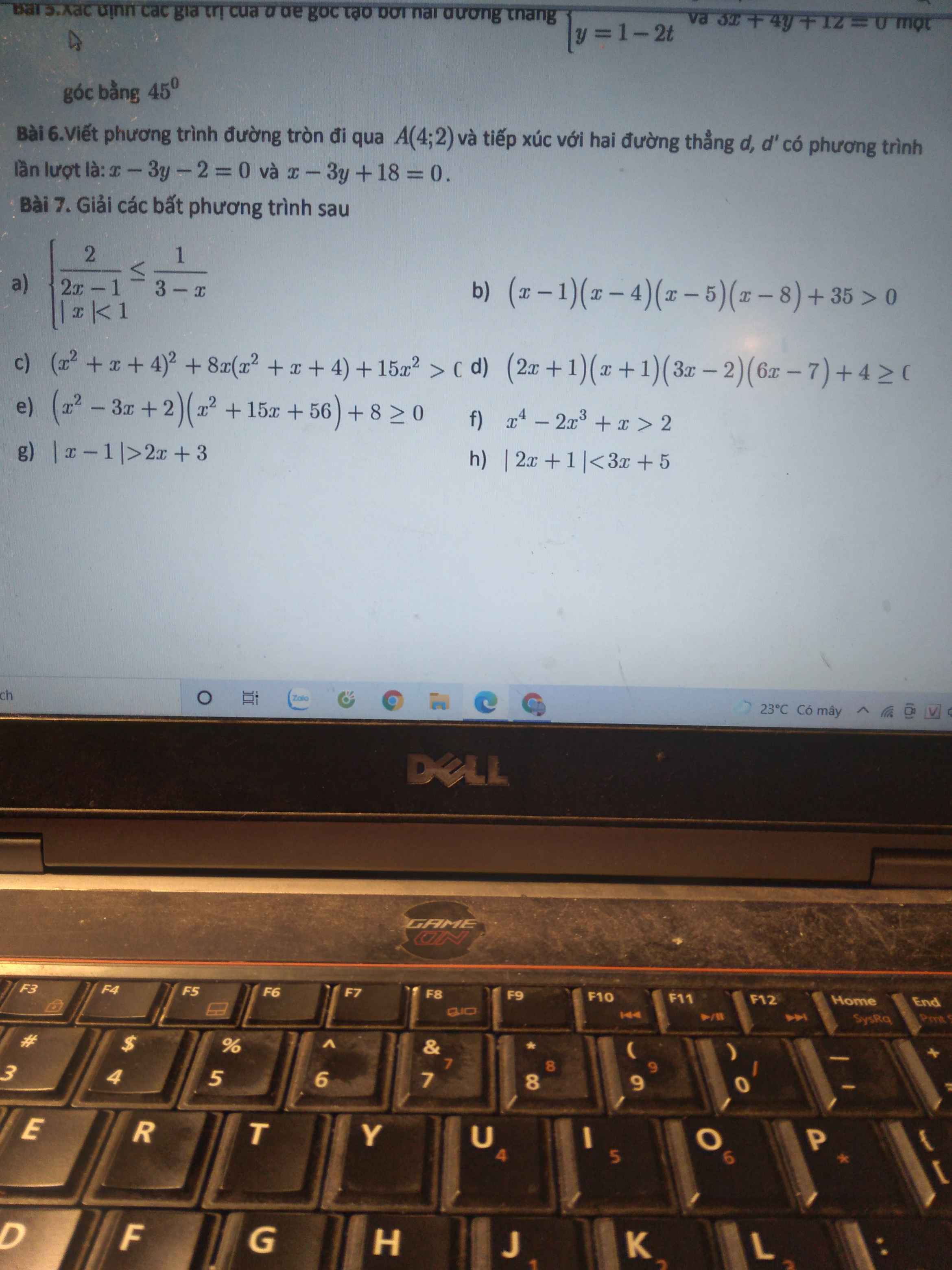
\(\left(x\ne3;x\ne\dfrac{1}{2}\right)\)\(\left\{{}\begin{matrix}\dfrac{2}{2x-1}\le\dfrac{1}{3-x}\\\left|x\right|< 1\Leftrightarrow-1< x< 1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2\left(3-x\right)-2x+1}{\left(2x-1\right)\left(3-x\right)}\le0\left(1\right)\\-1< x< 1\end{matrix}\right.\)\(\)
\(\left(1\right)\Leftrightarrow\dfrac{-4x+7}{\left(2x-1\right)\left(3-x\right)}\le0\)\(\Leftrightarrow\dfrac{-4x+7}{-2x^2+7x-3}\le0\Leftrightarrow x\in\left(-\infty;\dfrac{1}{2}\right)\cup[\dfrac{7}{4};3)\)
\(kết\) \(hợp:-1< x< 1\)\(\Rightarrow x\in\left(-1;\dfrac{1}{2}\right)\cup[\dfrac{7}{4};3)\)
\(b,\)\(\left(x-1\right)\left(x-4\right)\left(x-5\right)\left(x-8\right)+35>0\)
\(\Leftrightarrow\left(x^2-9x+8\right)\left(x^2-9x+20\right)+35>0\)
\(đặt:x^2-9x+8=t\ge-\dfrac{49}{4}\)
\(bpt\Leftrightarrow t\left(t+12\right)+35>0\Leftrightarrow t^2+12t+35>0\Leftrightarrow\left[{}\begin{matrix}t< -7\\t>-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-9x+8< -7\\x^2-9x+8>-5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{9-\sqrt{21}}{2}< x< \dfrac{9+\sqrt{21}}{2}\\x\in\left(-\infty;\dfrac{9-\sqrt{29}}{2}\right)\cup\left(\dfrac{9+\sqrt{29}}{2};+\infty\right)\end{matrix}\right.\)
\(c;\)\(\left(x^2+x+4\right)^2+2.4x\left(x^2+x+4\right)+16x^2-x^2>0\)
\(\Leftrightarrow\left(x^2+x+4+4x\right)^2-x^2>0\)
\(\Leftrightarrow\left(x+2\right)^2\left(x^2+6x+4\right)>0\)
\(\Leftrightarrow x^2+6x+4>0\Leftrightarrow....\)
ý d; giống ý b
\(e;bpt\Leftrightarrow\left(x-2\right)\left(x-1\right)\left(x+7\right)\left(x+8\right)+8>0\)
\(\Leftrightarrow\left(x^2+6x-16\right)\left(x^2+6x-7\right)+8>0\)
\(đặt:x^2+6x-7=t\ge-16\Rightarrow t\left(t-9\right)+8>0\)
(làm giống ý b)
\(f;x^4-2x^3+x-2>0\Leftrightarrow\left(x+1\right)\left(x-2\right)\left(x^2-x+1\right)>0\left(do:x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\right)\)
\(\Rightarrow bpt\Leftrightarrow\left(x+1\right)\left(x-2\right)>0\Leftrightarrow\left[{}\begin{matrix}x< -1\\x>2\end{matrix}\right.\)
\(g;h\) dùng bảng phá giá trị tuyệt đối để làm
Đúng 0
Bình luận (0)
Bài 1: so sánh
a> 3√7 và √28 ( làm 2 cách)
#e đg cần gấp giúp e vs ạ e cảm ơn
\(\left(3\sqrt{7}\right)^2=63>28=\left(\sqrt{28}\right)^2\) hoặc \(3\sqrt{7}>2\sqrt{7}=\sqrt{28}\)
Đúng 3
Bình luận (1)
C1: $\sqrt{28}=\sqrt{4.7}=2\sqrt 7$
Ta có: $3>2$
$\Leftrightarrow 3\sqrt 7>3\sqrt 7$ hay $3\sqrt 7>\sqrt{28}$
C2: $3\sqrt{7}=\sqrt{63}$
Ta có: $63>28$
$\Leftrightarrow\sqrt{63}>\sqrt{28}$ hay $3\sqrt 7>\sqrt{28}$
Đúng 2
Bình luận (2)




















