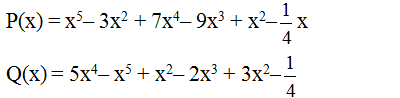đa thức p(x) và Q(x) đâu bạn

thay x=0 vào mà tính là đc

a: Ta có: \(P=x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)

\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)

Ta có: \(Q=5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)

\(=-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)

\(P\left(0\right)=3.0^4+0^3-0^2+\dfrac{1}{4}.0=0+0-0+0=0\)

\(Q\left(0\right)=0^4-4.0^3+0^2-4=0-0+0-4=-4\)

vậy Chứng tỏ x=0 là nghiệm của đa thức P(x), nhưng không phải là nghiệm của đa thức Q(x)

thu gọn

\(P\left(x\right)=3x^4+x^3\left(-2x^2+x^2\right)+\dfrac{1}{4}x=3x^4+x^3-x^2+\dfrac{1}{4}x\)

\(Q\left(x\right)=x^4-4x^3+\left(3x^2-2x^2\right)-4=x^4-4x^3+x^2-4\)

Lời giải:
Ta thấy:

$P(0)=-2.0^2+3.0^4+0^3+0^2-\frac{1}{4}.0=0$ nên $x=0$ là nghiệm của $P(x)$

$Q(0)=0^4+3.0^2-4-4.0^3-2.0^2=-4\neq 0$

Do đó $x=0$ không phải nghiệm của $Q(x)$

a) Sắp xếp theo lũy thừa giảm dần

P(x)=x^5−3x^2+7x^4−9x^3+x^2−1/4x

=x^5+7x^4−9x^3−3x^2+x^2−1/4x

=x^5+7x^4−9x^3−2x^2−1/4x

Q(x)=5x^4−x^5+x^2−2x^3+3x^2−1/4

=−x^5+5x^4−2x^3+x^2+3x^2−1/4

=−x^5+5x^4−2x^3+4x^2−1/4

b)

P(x)+Q(x)

=(x^5+7x^4−9x^3−2x^2−1/4^x)+(−x^5+5x^4−2x^3+4x^2−1/4)

=x^5+7x^4−9x^3−2x^2−1/4x−x^5+5x^4−2x^3+4x^2−1/4

=(x^5−x^5)+(7x^4+5x^4)+(−9x^3−2x^3)+(−2x^2+4x^2)−1/4x−1/4

=12x^4−11x^3+2x^2−1/4x−1/4

P(x)−Q(x)

=(x^5+7x^4−9x^3−2x^2−1/4x)−(−x^5+5x^4−2x^3+4x^2−1/4)

=x^5+7x^4−9x^3−2x^2−1/4x+x^5−5x^4+2x^3−4x^2+1/4

=(x^5+x^5)+(7x^4−5x^4)+(−9x^3+2x^3)+(−2x^2−4x^2)−1/4x+1/4

=2x5+2x4−7x3−6x2−1/4x−1/4

c) Ta có

P(0)=0^5+7.0^4−9.0^3−2.0^2−1/4.0

⇒x=0là nghiệm của P(x).

Q(0)=−0^5+5.0^4−2.0^3+4.0^2−1/4=−1/4≠0

⇒x=0không phải là nghiệm của Q(x).

Cho 2 đa thức: f(x)= 9 - x5 + 4x - 2x3 + x2 - 7x4

g(x)= x5 - 9 + 2x2 + 7x4 + 2x3 - 3x

a) Sắp sếp các đa thức trên theo luỹ thừa giảm dần của biến

f(x)= 9 - x5 + 4x - 2x3 + x2 - 7x4

f(x) = -x5 - 7x4 - 2x3 + x2 + 4x + 9

g(x)= x5 - 9 + 2x2 + 7x4 + 2x3 - 3x

g(x) = x5 + 7x4 + 2x3 + 2x2 - 3x - 9

b) Tìm bậc, hệ số cao nhất, hệ số tự do của đa thức f(x); g(x)

f(x) = -x5 - 7x4 - 2x3 + x2 + 4x + 9

+ Bậc : 5 _ hệ số cao nhất : -1 _ hệ số tự do : 9

g(x) = x5 + 7x4 + 2x3 + 2x2 - 3x - 9

+ Bậc : 5_ hệ số cao nhất : 1 _ hệ số tự do : -9

c) Tính f(x) + g(x); f(x) - g(x)

f( x) + g(x) = ( -x5 - 7x4 - 2x3 + x2 + 4x + 9 ) +( x5 + 7x4 + 2x3 + 2x2 - 3x - 9 )

= -x5 - 7x4 - 2x3 + x2 + 4x + 9 + x5 + 7x4 + 2x3 + 2x2 - 3x - 9

= ( -x5 + x5 ) + ( -7x4 + 7x4 ) + ( -2x3 + 2x3 ) + ( x2 + 2x2 ) + ( 4x -3x ) + ( 9 - 9 )

= 3x2 + x

f( x) - g(x) = ( -x5 - 7x4 - 2x3 + x2 + 4x + 9 ) - ( x5 + 7x4 + 2x3 + 2x2 - 3x - 9 )

= -x5 - 7x4 - 2x3 + x2 + 4x + 9 - x5 - 7x4 - 2x3 - 2x2 + 3x + 9

= ( -x5 - x5 ) + ( -7x4 - 7x4 ) + ( -2x3 - 2x3 ) + ( x2 - 2x2 ) + ( 4x + 3x ) + ( 9 + 9 )

= -2x5 - 14x4 - 2x3 -x2 + 7x + 18

a) P(x) = x⁵ - 3x² + 7x⁴ - 9x³ + x² - 14x

            = x⁵ + 7x⁴ - 9x³ - 2x² - 14x

Q(x) = 5x⁴ - x⁵ + x² - 2x³ + 3x² -14

        = -x⁵ + 5x⁴ - 2x³ + 4x² - 14

b) P(x) + Q(x) =  x⁵ + 7x⁴ - 9x³ - 2x² - 14x - x⁵ + 5x⁴ - 2x³ + 4x² - 14

                       = 12x⁴ - 11x³ + 2x² - 14x - 14

P(x) - Q(x) = ( x⁵ + 7x⁴ - 9x³ - 2x² - 14x ) - ( -x⁵ + 5x⁴ - 2x³ + 4x² - 14 )

                  = x⁵ + 7x⁴ - 9x³ - 2x² - 14x + x⁵ - 5x⁴ + 2x³ - 4x² + 14

                  = 2x⁵ + 2x⁴ - 7x³ - 6x² - 14x + 14

c) P(0) = 0⁵ + 7.0⁴ - 9.0³ - 2.0² - 14.0 = 0 

=> x = 0 là nghiệm của P(x)

Q(0) = -0⁵ + 5.0⁴ - 2.0³ + 4.0² - 14 = 0 - 14 = -14\(\ne\)0

=> x = 0 không phải là nghiệm của Q(x) 

$\rm x=1\\\to ax^2+bx+c=a+b+c=0\\\to x=1\,\là \,\,no \,\pt$

`x=-1=>ax^2+bx+c=a-b+c=0`

1.P(x)= -Q(x)

=>3x³+x²-3x-1=3x³+x²+x+15

=>4x= -16 => x= -4

2.Ta có:P(1)=0 và Q(1) khác 0

=>điều phải chứng minh