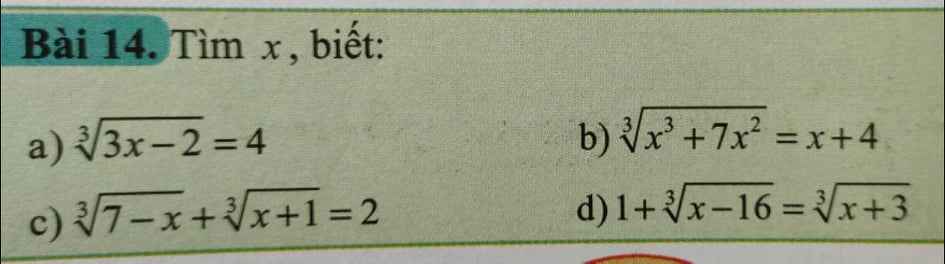 Giải giúp a b
Giải giúp a b

Những câu hỏi liên quan
Cho phân số: 1>a/b hãy so sánh a/b với a+m/b+m
Mọi người giải gấp giúp em với ạ ai giải xong trước em tích cho ạ
Mọi người diễn giải ra giúp em vs ạ
ab = a : b
a+m/b+m = (a + m) : (b + m)
a+m/b+m >a /b
tìm a∩b,a∪b,a\b,b\a: a=(-∞;+∞),b=(1;7] Các bạn giải nhanh giúp mình
\(A=\left(-\infty;+\infty\right);B=(1;7]\)
\(A\cap B=(1;7]\)
\(A\cup B=\left(-\infty;+\infty\right)\)
\(A\backslash B=(-\infty;1]\cup\left(7;+\infty\right)\)
\(B\text{A}=\varnothing\)
Đúng 0
Bình luận (0)
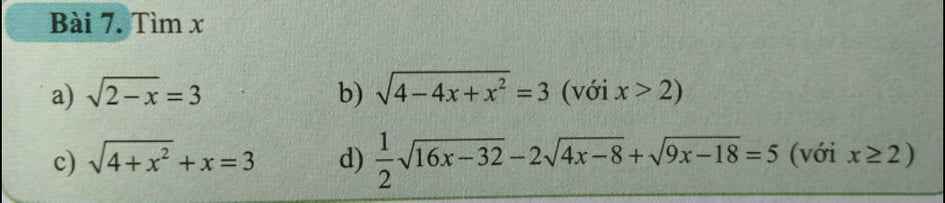 Giải giúp a b
Giải giúp a b
a) ĐK: x ≤ 2
PT <=> 2 - x = 9
,=> x = -7
b) PT <=> \(\sqrt{\left(2-x\right)^2}=3\)
<=> 2 - x = 3
<=> x = -1
c) PT <=> \(\sqrt{4+x^2}=3-x\)
\(\Leftrightarrow4+x^2=9-6x+x^2\)
\(\Leftrightarrow-6x+5=0\)
\(\Leftrightarrow x=\dfrac{5}{6}\)
d) PT <=> \(\dfrac{1}{2}\sqrt{16\left(x-2\right)}-2\sqrt{4\left(x-2\right)}+\sqrt{9\left(x-2\right)}=5\)
\(\Leftrightarrow\dfrac{1}{2}.4.\sqrt{x-2}-2.2.\sqrt{x-2}+3.\sqrt{x-2}=5\)
\(\Leftrightarrow\sqrt{x-2}\left(\dfrac{1}{2}.4-2.2+3\right)=5\)
\(\Leftrightarrow\sqrt{x-2}=5\)
\(\Leftrightarrow x-2=25\)
<=> x = 27
Đúng 1
Bình luận (0)
a) \(\sqrt[]{2-x}\) = 3
⇔ 2 - x = 9
⇔ x = -7
vậy....
b)\(\sqrt{4-4x+x^2}\) =3
⇔ \(\sqrt{\left(2-x\right)^2}\) =3
⇔ I2 - xI=3
⇔ x - 2 = 3 (vì x>2)
⇔ x = 5
vậy.....
Đúng 0
Bình luận (0)
 giải giúp a b
giải giúp a b
a)\(6\sqrt[3]{81}-4\sqrt[3]{375}+3\sqrt[3]{24}\)
\(=6\sqrt[3]{3^4}-4\sqrt[3]{3.5^3}+3\sqrt[3]{3.2^3}\)
\(=6.3\sqrt[3]{3}-4.5\sqrt[3]{3}+3.2\sqrt[3]{3}=4\sqrt[3]{3}\)
b)\(\sqrt[3]{3}.\sqrt[3]{144}-\dfrac{\sqrt[3]{384}}{\sqrt[3]{3}}+2\sqrt[3]{-128}\)
\(=\sqrt[3]{432}-\sqrt[3]{\dfrac{384}{3}}+2\sqrt[3]{-2.4^3}\)
\(=\sqrt[3]{6^3.2}-\sqrt[3]{2.4^3}+2.\sqrt[3]{-2.4^3}\)
\(=6\sqrt[3]{2}-4\sqrt[3]{2}+2.-4\sqrt[3]{2}==-6\sqrt[3]{2}\)
Đúng 2
Bình luận (0)
 giải giúp a b
giải giúp a b
a) Ta có: \(\sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}\)
\(=\dfrac{\sqrt{6+2\sqrt{5}}+\sqrt{6-2\sqrt{5}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{5}+1+\sqrt{5}-1}{\sqrt{2}}=\dfrac{2\sqrt{5}}{\sqrt{2}}=\sqrt{10}\)
b) Ta có: \(2\sqrt{2}\left(\sqrt{3}-2\right)+\left(9+4\sqrt{2}\right)\)
\(=2\sqrt{6}-4\sqrt{2}+9+4\sqrt{2}\)
\(=9+2\sqrt{6}\)
c) Ta có: \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\left(2+\sqrt{3}\right)}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{28-10\sqrt{3}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\left(5-\sqrt{3}\right)}}\)
\(=\sqrt{4+\sqrt{25}}=\sqrt{4+5}=3\)(đpcm)
Đúng 1
Bình luận (1)
tìm a,b ϵ N, biết [a,b]+(a,b)=23
giải giúp tớ với
\(\left[a,b\right]+\left(a,b\right)=23\\ a,b=23:2\\ a,b=11,5\\ \Rightarrow a=11\\ b=5\)
Đúng 1
Bình luận (0)
Ta có : Vì [a,b] chia hết cho (a,b) Và (a,b) chia hết cho (a,b) =)[a,b]+(a,b) chia hết cho (a,b) =)23 chia hết cho (a,b) =)(a,b) thuộc Ư(23)={1,23} +)nếu (a,b)=1 =)[a,b]=23-1=22 =)a.b=1.22=22 Với a,b là số nguyên tố cùng nhau và a.b =22 .Giả sử a>b =)a=22,b=1(TM) Và a=11,b=2(TM) +)nẾU (a,b)=23 =0 [a,b]=23-23=0(Loại vì a,b khác o)
CHÚC HỌC TỐT
Đúng 1
Bình luận (0)
Giải giúp mình với : So sánh A và B
A=31 x H5 - 30 và B=15+30xH5
- Giúp mình nhé! Ai giải được mình bảo gì mình làm đấy
Mọi người giúp em câu d hình với ạ. Câu a, b, c em giải được rồi.Lời giải câu a,b,c của em:
Đọc tiếp

Mọi người giúp em câu d hình với ạ. Câu a, b, c em giải được rồi.
Lời giải câu a,b,c của em:
Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng
Đúng 0
Bình luận (0)
Tìm a,b là 2 số tự nhiên biết : BCNN (a,b ) + ƯCLN (a,b ) = 19
GIẢI RÕ RA HỘ NHA .GIẢI GIÚP EM NHA




















