a) \(\sqrt[3]{3x-2}=4\Rightarrow3x-2=64\Rightarrow3x=66\Rightarrow x=22\)
b) \(\sqrt[3]{x^3+7x^2}=x+4\Rightarrow x^3+7x^2=\left(x+4\right)^3\)
\(\Rightarrow x^3+7x^2=x^3+12x^2+48x+64\Rightarrow5x^2+48x+64=0\)
\(\Rightarrow\left(x+8\right)\left(5x+8\right)=0\Rightarrow\left[{}\begin{matrix}x=-8\\x=-\dfrac{8}{5}\end{matrix}\right.\)
a) Ta có: \(\sqrt[3]{3x-2}=4\)
\(\Leftrightarrow3x-2=64\)
\(\Leftrightarrow3x=66\)
hay x=22
b) Ta có: \(\sqrt[3]{x^3+7x^2}=x+4\)
\(\Leftrightarrow x^3+7x^2=\left(x+4\right)^3\)
\(\Leftrightarrow x^3+7x^2-x^3-12x^2-48x-64=0\)
\(\Leftrightarrow-5x^2-48x-64=0\)
\(\Leftrightarrow5x^2+48x+64=0\)
\(\text{Δ}=48^2-4\cdot5\cdot64=1024\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-48-32}{10}=\dfrac{-80}{10}=-8\\x_2=\dfrac{-48+32}{10}=\dfrac{-16}{10}=\dfrac{-8}{5}\end{matrix}\right.\)

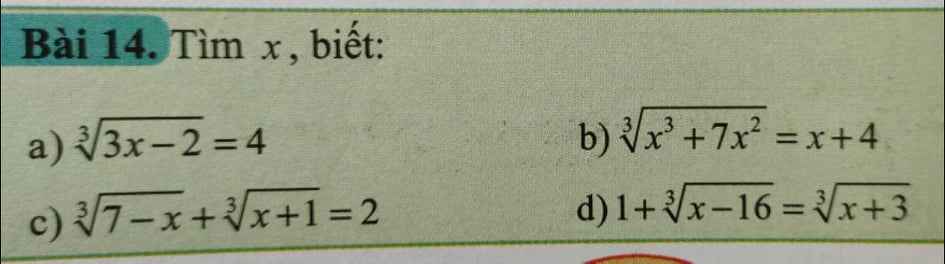 Giải giúp a b
Giải giúp a b




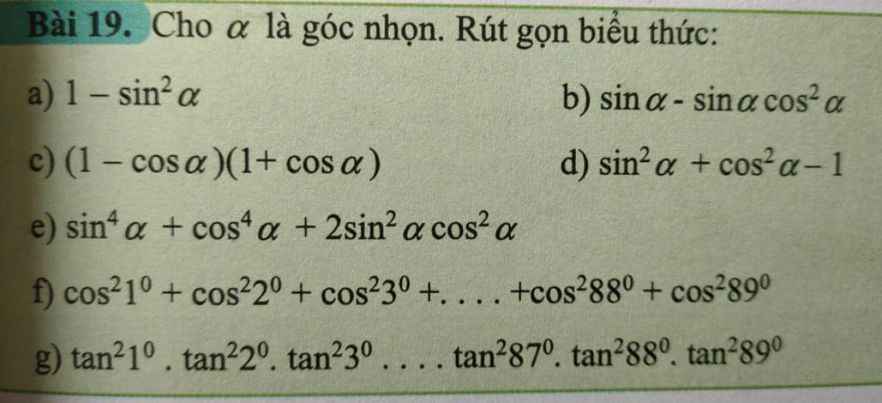 Giải chi tiết giúp a b c
Giải chi tiết giúp a b c



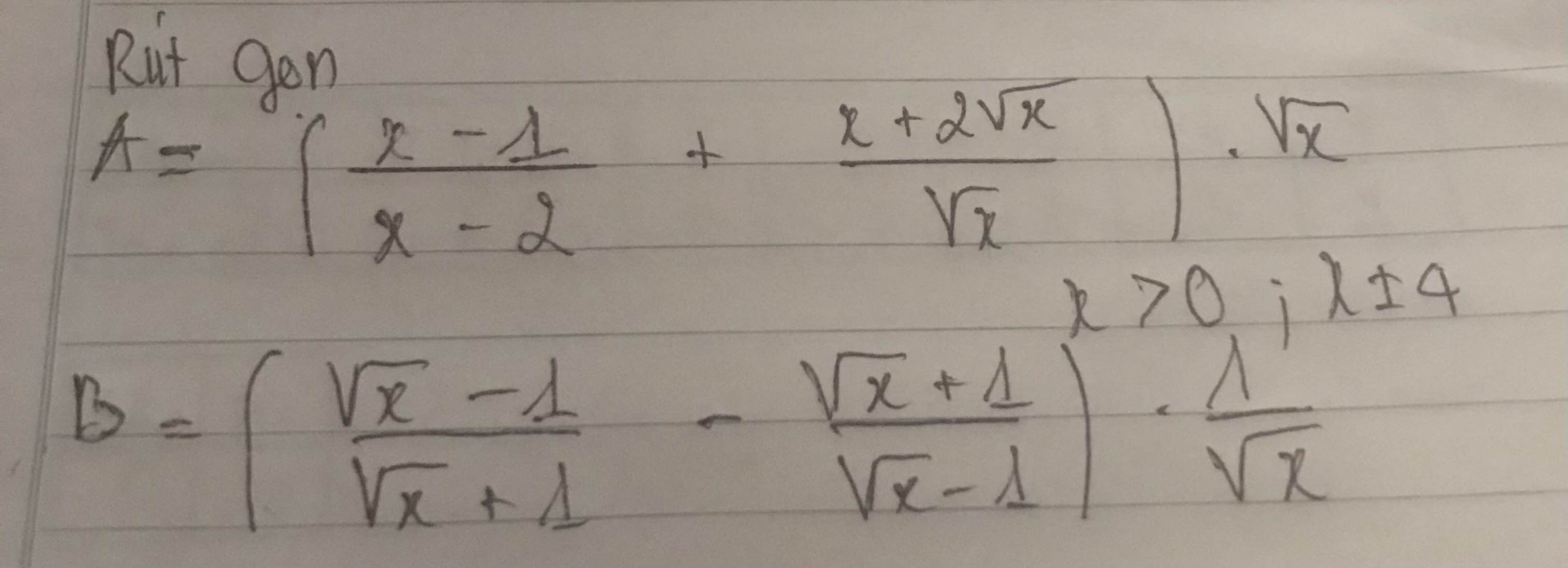



 Giải giúp bài 3 a nha thầy tui bảo đặt mẫu số là b rồi đặt nhân tử chung.Thầy bảo tui làm ko cho hỏi Giải giúp
Giải giúp bài 3 a nha thầy tui bảo đặt mẫu số là b rồi đặt nhân tử chung.Thầy bảo tui làm ko cho hỏi Giải giúp
