( 2x -3 )^2
Giúp mik vs mng
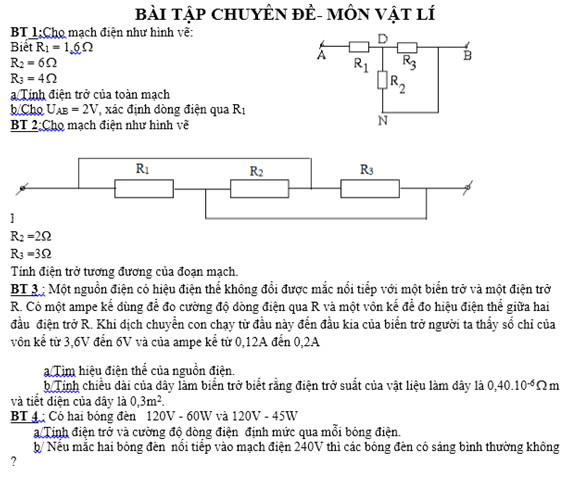 mng giúp mik bài 1 vs bài 3 vs, mik cần gấp lắm, cảm ơn mng.
mng giúp mik bài 1 vs bài 3 vs, mik cần gấp lắm, cảm ơn mng.
giúp mik vs mng ơi!
CM đa thức M(x)= x2 +2x + 2022 ko có nghiệm
Cho `M(x)=0`
`=>x^2+2x+2022=0`
`=>x^2+2x+1+2021=0`
`=>(x+1)^2=-2021` (Vô lí vì `(x+1)^2 >= 0` mà `-2021 < 0`)
Vậy đa thức `M(x)` không có nghiệm
Ta có M(x) = x2 + 2x + 2022
= x2 + x + x + 1 + 2021
= x(x + 1) + (x + 1) + 2021
= (x+1) . (x+1) + 2021
= (x+1)2 + 2021
Ta có ( x + 1)2 \(\ge\)0
2021 > 0
=> (x+1)2 + 2021 > 0
=> x2 + 2x + 2022> 0
Vậy đa thức trên không có nghiệm
M(x)= x2 +2x + 2022
\(M\left(x\right)=x^2+x+x+1+2021\)
\(M\left(x\right)=x\left(x+1\right)+\left(x+1\right)+2021\)
\(M\left(x\right)=\left(x+1\right)\left(x+1\right)+2021=\left(x+1\right)^2+2021\)
ta có \(\left(x+1\right)^2\ge0\forall x\)
mà 2021 > 0
\(=>\left(x+1\right)^2+2021>0\)
hay M(x)= x2 +2x + 2022 ko có nghiệm
Mng ơi help vs, mik cần rất gấp, mong mng có thể giúp mik
2:
a: Xét tứ giác DIHK có
\(\widehat{DIH}=\widehat{DKH}=\widehat{IDK}=90^0\)
Do đó: DIHK là hình chữ nhật
Suy ra: DH=KI(1)
Xét ΔDEF vuông tại D có DH là đường cao ứng với cạnh huyền EF
nên \(DH^2=HE\cdot HF\left(2\right)\)
Từ (1) và (2) suy ra \(IK^2=HE\cdot HF\)
Mng làm nhanh giúp mik vs ah, mik đg cần gấp ah, ai nhanh mik tik nha <3
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
Tìm tất cả giá trị x,y nguyên thỏa mãn: 16 - 3(y - 3)2 = (2023-x)2
Giúp mik vs mng oiiiiiiii
Lời giải:
Do $(2023-x)^2\geq 0$ với mọi $x$ nên:
$3(y-3)^2=16-(2023-x)^2\leq 16<18$
$\Rightarrow (y-3)^2< 6$
Mà $(y-3)^2\geq 0$ và $(y-3)^2$ là số chính phương với mọi $y$ nguyên.
$\Rightarrow (y-3)^2=0$ hoặc $(y-3)^2=4$
Nếu $(y-3)^2=0$ thì $y=3$.
Khi đó: $(2023-x)^2=16-3.0^2=16$
$\Rightarrow 2023-x=4$ hoặc $2023-x=-4$
$\Rightarrow x=2019$ hoặc $x=2027$
Nếu $(y-3)^2=4\Rightarrow y-3=2$ hoặc $y-3=-2$
$\Rightarrow y=5$ hoặc $y=1$
Khi đó:
$(2023-x)^2=16-3.4=4=2^2=(-2)^2$
$\Rightarrow 2023-x=2$ hoặc $2023-x=-2$
$\Rightarrow x=2021$ hoặc $x=2025$
Em hãy thuyết minh về đại hội thể dục thể thao ở địa phương em.
Mng giúp mik vs ạ, mik đag cần rất gấp.
Cảm ơn mng nhìu <3
mng giúp mình vs ạ,mik cần gấp.Cảm ơn mng nhiều
a, Theo tc 2 tt cắt nhau: \(AE=EC;BF=CF\)
Vậy \(AE+BF=EC+CF=EF\)
b, Vì \(\left\{{}\begin{matrix}AE=EC\\\widehat{EAO}=\widehat{ECO}=90^0\\OE.chung\end{matrix}\right.\) nên \(\Delta AOE=\Delta COE\)
\(\Rightarrow\widehat{AOE}=\widehat{EOC}\) hay OE là p/g \(\widehat{AOC}\)
Cmtt: \(\Delta BOF=\Delta COF\Rightarrow\widehat{BOF}=\widehat{COF}\) hay OF là p/g \(\widehat{BOC}\)
Vậy \(\widehat{EOF}=\widehat{COF}+\widehat{COE}=\dfrac{1}{2}\left(\widehat{AOC}+\widehat{BOC}\right)=90^0\) hay OE⊥OF
Cho tổng S = 4 + 3^2 + 3^3 + 3^4 + ... + 3^223.
Chứng minh rằng tổng S chia hết cho 41?
mng giúp mik vs
S=4+32+33+...+3223
S=1+3+32+33+...+3223
S=(1+34)+(3+35)+(32+36)+(33+37)+...+(3119+3223)
S=82+3(1+34)+32(1+34)+33(1+34)+...+3119(1+34)
S=82+3.82+32.82+33.82+...+3119.(1+34)
S=82(3+32+33+...+3119)
vì 82⋮41⇒S⋮41
Vậy S⋮41
cho hàm số y=5-2x
a) Vẽ đths trên
b) Tính góc tạo bởi đths trên vs Ox
c) Tính khoảng cách từ tọa độ O (0;0) đths
Giúp mik vs mng ơiiii TT.TT