
Ai học giỏi Tiếng Anh giúp e làm bài này với ạ !!? E đang cần gấp ![]()
Anh chị ơi giúp e làm bài này với ạ, e cần gấp ý ạ:(( E cảm ơn các anh chị nhiều ạ<3

Bài 6
\(a,ĐK:x\ne\pm5\\ b,P=\dfrac{x-5+2x+10-2x-10}{\left(x-5\right)\left(x+5\right)}=\dfrac{x-5}{\left(x-5\right)\left(x+5\right)}=\dfrac{1}{x+5}\\ c,P=-3\Leftrightarrow\dfrac{1}{x+5}=-3\Leftrightarrow-3\left(x+5\right)=1\Leftrightarrow x=-\dfrac{16}{3}\\ \Leftrightarrow Q=\left(3x-7\right)^2=\left[3\cdot\left(-\dfrac{16}{3}\right)-7\right]^2=529\)
Bài 7:
\(a,ĐK:x\ne\pm3\\ b,P=\dfrac{3x-9+x+3+18}{\left(x-3\right)\left(x+3\right)}=\dfrac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{4}{x-3}\\ b,P=4\Leftrightarrow4\left(x-3\right)=4\Leftrightarrow x=4\)
Điều kiện (x≠5, x≠-5)
\(P=\dfrac{1}{x+5}+\dfrac{2}{x-5}-\dfrac{2x+10}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{x-5}{\left(x+5\right)\left(x-5\right)}+\dfrac{2\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}-\dfrac{2\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{x-5+2\left(x+5\right)-2\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{x-5}{\left(x+5\right)\left(x-5\right)}=\dfrac{1}{x+5}\)
Anh chị ơi giúp em làm bài này với ạ! E đg cần gấp lắm luôn ý:(( E cảm ơn anh chị nhiều ạ<3

\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)
Bào quan riboxom trong chất tế bào có chức năng gì?
a) \(=\left(x^2+x\right)+\left(4x+4\right)=x\left(x+1\right)+4\left(x+1\right)=\left(x+1\right)\left(x+4\right)\)
b) \(=\left(x^2+2x\right)-\left(3x+6\right)=x\left(x+2\right)-3\left(x+2\right)=\left(x+2\right)\left(x-3\right)\)
c) \(=\left(x^2-2x\right)-\left(3x-6\right)=x\left(x-2\right)-3\left(x-2\right)=\left(x-2\right)\left(x-3\right)\)
d) \(3x^2+9x-30=3\left(x^2+3x-10\right)=3\left[\left(x^2+5x\right)-\left(2x+10\right)\right]=3\left[x\left(x+5\right)-2\left(x+5\right)\right]=3\left(x-2\right)\left(x+5\right)\)
e) \(=-\left(3x^2-5x-2\right)=-\left[\left(3x^2-6x\right)+\left(x-2\right)\right]=-\left[3x\left(x-2\right)+\left(x-2\right)\right]=-\left(3x+1\right)\left(x-2\right)\)
f) \(x^2-7x+6=\left(x^2-x\right)-\left(6x-6\right)=x\left(x-1\right)-6\left(x-1\right)=\left(x-1\right)\left(x-6\right)\)
h) \(=4\left(x^2-9x+14\right)=4\left[\left(x^2-7x\right)-\left(2x-14\right)\right]=4\left[x\left(x-7\right)-2\left(x-7\right)\right]=4\left(x-2\right)\left(x-7\right)\)
i) \(=3\left(3x^2-8x+5\right)=3\left[\left(3x^2-3x\right)-\left(5x-5\right)\right]=3\left[3x\left(x-1\right)-5\left(x-1\right)\right]=3\left(x-1\right)\left(3x-5\right)\)
k) \(=-\left(2x^2+5x+2\right)=-\left[\left(2x^2+4x\right)+\left(x+2\right)\right]=-\left[2x\left(x+2\right)+\left(x+2\right)\right]=-\left(x+2\right)\left(2x+1\right)\)
l) \(=\left(x^2-5xy\right)-\left(2xy-10y^2\right)=x\left(x-5y\right)-2y\left(x-5y\right)=\left(x-5y\right)\left(x-2y\right)\)
m) \(=\left(x^2-2xy\right)-\left(xy-2y^2\right)=x\left(x-2y\right)-y\left(x-2y\right)=\left(x-2y\right)\left(x-y\right)\)
n) \(=\left(x^2-3xy\right)+\left(xy-3y^2\right)=x\left(x-3y\right)+y\left(x-3y\right)=\left(x+y\right)\left(x-3y\right)\)
Bài khó quá nên nhờ ai học giỏi làm giúp em ạ! Em đang cần gấp :(
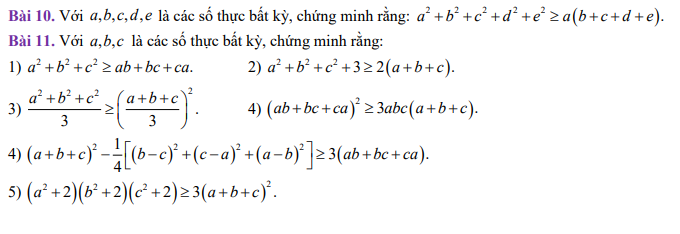
\(10,\\ a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\\ \Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2\ge4ab+4ac+4ad+4ae\\ \Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-4ac+4c^2\right)+\left(a^2-4ad+4d^2\right)+\left(a^2-4ae+4e^2\right)\ge0\\ \Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2e\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow\dfrac{a}{2}=b=c=d=e\)
\(4,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{4}\left(2a^2+2b^2+2c^2-2ab-2ac-2bc\right)\ge3ab+3bc+3ca\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{2}a^2-\dfrac{1}{2}b^2-\dfrac{1}{2}c^2-ab-bc-ac\ge0\\ \Leftrightarrow\dfrac{1}{2}a^2+\dfrac{1}{2}b^2+\dfrac{1}{2}c^2+ab+ac+bc\ge0\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge0\\ \Leftrightarrow\left(a+b+c\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a+b+c=0\)
\(1,a^2+b^2+c^2\ge ab+bc+ca\\ \Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc\ge0\\ \Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)\ge0\\ \Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b=c\)
\(2,a^2+b^2+c^2+3\ge2\left(a+b+c\right)\\ \Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+\left(c^2-2c+1\right)\ge0\\ \Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b=c=1\)
\(3,\Leftrightarrow\dfrac{a^2+b^2+c^2}{3}\ge\dfrac{\left(a+b+c\right)^2}{9}\\ \Leftrightarrow9\left(a^2+b^2+c^2\right)\ge3\left(a+b+c\right)^2\\ \Leftrightarrow3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\\ \Leftrightarrow3a^2+3b^2+3c^2-a^2-b^2-c^2-2ab-2ac-2bc\ge0\\ \Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc\ge0\left(luôn.đúng.do.câu.1\right)\)
Dấu \("="\Leftrightarrow a=b=c\)
\(4,\Leftrightarrow a^2b^2+b^2c^2+a^2c^2+2a^2bc+2ab^2c+2abc^2\ge3a^2bc+3ab^2c+3abc^2\\ \Leftrightarrow a^2b^2+b^2c^2+a^2c^2-a^2bc-ab^2c-abc^2\ge0\\ \Leftrightarrow2a^2b^2+2b^2c^2+2a^2c^2-2a^2bc-2ab^2c-2abc^2\ge0\\ \Leftrightarrow\left(a^2b^2-2a^2bc+a^2c^2\right)+\left(a^2b^2-2ab^2c+b^2c^2\right)+\left(b^2c^2-2abc^2+a^2c^2\right)\ge0\\ \Leftrightarrow\left(ab-ac\right)^2+\left(ab-bc\right)^2+\left(bc-ac\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow ab=bc=ac\)
Giải giúp e bài hình này với ạ
E đang cần gấp ạ , e cảm ơn

a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12

ANh chị ơi giúp e giải bài này với ạ! E đg cần gấp ý:(( E cảm ơn anh chị nhiều ạ<3
Mn giải giúp e bài này với ạ. E đang cần gấp
Các anh chị em giúp em cái này vs ạ e đang cần lời giới thiệu trong buổi diễn văn nghệ nhân dịp 20 - 11 cho bài vui đến trường cần gấp hôm nay ai giúp đỡ em vs ạ
Mọi người giúp em trả lời hai bài tiếng anh này với em đang cần gấp lắm ạ.

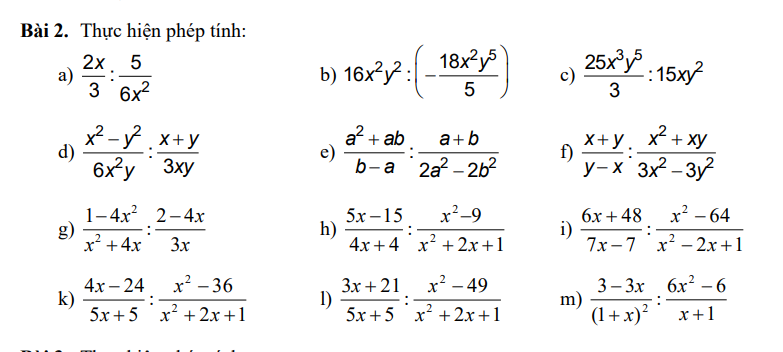
Anh chị ui giúp e làm bài này với ạ! E đg cần gắp lắm ý:(( Em cảm ơn anh chị nhiều ạ<3