Lời giải:

$\frac{S_{AMN}}{S_{ANB}}=\frac{AM}{AB}=\frac{1}{2}$

Suy ra $S_{AMN}=\frac{1}{2}\times S_{ANB}$

$\frac{S_{ABN}}{S_{ABC}}=\frac{AN}{AC}=\frac{1}{3}$

$\Rightarrow S_{ABN}=\frac{1}{3}S_{ABC}$

Suy ra $S_{AMN}=\frac{1}{2}\times \frac{1}{3}\times S_{ABC}$

$\Rightarrow 6=\frac{1}{6}\times S_{ABC}$

$\Rightarrow S_{ABC}=36$ (cm²)

\(\dfrac{S_{ABC}}{S_{AMN}}=\dfrac{\dfrac{1}{2}AB.AC.sinA}{\dfrac{1}{2}AM.AN.sinA}=\dfrac{AB.AC}{\dfrac{1}{2}AB.\dfrac{2}{3}AC}=3\)

\(AN=\dfrac{2}{3}AC\Rightarrow CN=\dfrac{1}{3}AC\)

\(\dfrac{S_{CBN}}{S_{ABC}}=\dfrac{\dfrac{1}{2}CN.CB.sinC}{\dfrac{1}{2}CA.CB.sinC}=\dfrac{\dfrac{1}{3}CA}{CA}=\dfrac{2}{3}\)

\(S_{ABC}=S_{AMN}+S_{BNM}+S_{CBN}\)

\(\Rightarrow S_{BMN}=S_{ABC}-S_{AMN}-S_{CBN}=S_{ABC}-\dfrac{1}{3}S_{ABC}-\dfrac{1}{3}S_{ABC}=\dfrac{1}{3}S_{ABC}\)

\(\Rightarrow\dfrac{S_{ABC}}{S_{BMN}}=3\)

hk2 nha em chi hoc truoc chuong trinh

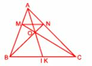
a) Vì AB = 3 x AM, AC = 3 x AN, nên MB = 2/3 x AB, NC = 2/3 x AC.

Từ đó suy ra : dt (MBC) = 2/3 x dt (ABC) (chung chiều cao từ C

dt (NCB) = 2/3 x dt (ABC) (chung chiều cao từ B)

Vậy dt (MBC) = dt (NCB) mà tam giác MBC và tam giác NCB có chung đáy BC, nên chiều cao từ M bằng chiều cao từ N xuống đáy BC hay MN song song với BC. Do đó BMNC là hình thang.

Từ MB = 2/3 x AB, nên dt (MBN) = 2/3 x dt (ABN) (chung chiều cao từ N) hay dt (ABN) = 2/3 x dt (MBN).

Hơn nữa từ AC = 3 x AN, nên NC = 2 x AN, do đó dt (NBC) = 2 x dt (ABN) (chung chiều cao từ B) ; suy ra dt (NBC) = 3/2 x 2 x dt (MBN) = 3 x dt (MBN).

Mà tam giác NBC và tam giác MBN có chiều cao bằng nhau (cùng là chiều cao của hình thang BMNC). Vì vậy đáy BC = 3 x MN.

b) Gọi BN cắt CM tại O. Ta sẽ chứng tỏ AI cũng cắt BN tại O. Muốn vậy, nối AO kéo dài cắt BC tại K, ta sẽ chứng tỏ K là điểm chính giữa của BC (hay K trùng với I).

Theo phần a) ta đã có dt (NBC) = 2 x dt (ABN). Mà tam giác NBC và tam giác ABN có chung đáy BN, nên chiều cao từ C gấp 2 lần chiều cao từ A xuống đáy BN. Nhưng đó là chiều cao tương ứng của hai tam giác BCO và BAO có chung đáy BO, vì vậy dt (BCO) = 2 x dt (BAO)

Tương tự ta cũng có dt (BCO) = 2 x dt (CAO).

Do đó dt (BAO) = dt (CAO). Hai tam giác BAO và CAO có chung đáy AO, nên chiều cao từ B bằng chiều cao từ C xuống đáy AO. Đó cũng là chiều cao tương ứng của hai tam giác BOK và COK có chung đáy OK, vì vậy dt (BOK) = dt (COK). Mà hai tam giác BOK và tam giác COK lại chung chiều cao từ O, nên hai đáy BK = CK hay K là điểm chính giữa của cạnh BC. Vậy điểm K trùng với điểm I hay BN, CM, AI cùng cắt nhau tại điểm O.

a) Xét tam giác APN và NPC có:
+ Đáy AN = 1/4 AC hay AN = 1/3 NC ( giả thiết)
+ Chung chiều cao hạ từ P
* Diện tích tam giác APN= 1/3 diện tích tam giác PNC
* Vậy diện tích PNC = 10 x 3 = 30(cm3)
b) Nối B với N
Xét tam giác PBM và tam giác MPC có:
+ Chung chiều cao hạ từ P xuống đáy BC
+ BM = MC ( theo giả thiết)
* Diện tích tam giác PBM = MPC (1)
Xét tam giác BNM và MNC có:
+ Chung chiều cao hạ từ N
+ BM = MC ( theo giả thiết)
* Diện tích tam giác BNM = MNC (2)
* Từ (1) và (2) ta có diện tích BPN = NPC ( hiệu hai tam giác bằng nhau)
* Diện tích BPN = 30 (cm2)

* Mà diện tích tam giác ANB = diện tích PNB – APN= 30- 10=20(cm²)
Xét tam giác ABN và ABC có:
+ AN = 1/4 AC ( giả thiết)
+ Chung chiều cao hạ từ B
* Diện tích tam giác ABN= 1/4 diện tích tam giác ABC = 20 x 4 = 80 (cm²)

80cm2

90cm2 nha