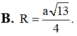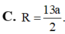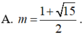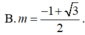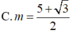\(\dfrac{S_{ABC}}{S_{AMN}}=\dfrac{\dfrac{1}{2}AB.AC.sinA}{\dfrac{1}{2}AM.AN.sinA}=\dfrac{AB.AC}{\dfrac{1}{2}AB.\dfrac{2}{3}AC}=3\)
\(AN=\dfrac{2}{3}AC\Rightarrow CN=\dfrac{1}{3}AC\)
\(\dfrac{S_{CBN}}{S_{ABC}}=\dfrac{\dfrac{1}{2}CN.CB.sinC}{\dfrac{1}{2}CA.CB.sinC}=\dfrac{\dfrac{1}{3}CA}{CA}=\dfrac{2}{3}\)
\(S_{ABC}=S_{AMN}+S_{BNM}+S_{CBN}\)
\(\Rightarrow S_{BMN}=S_{ABC}-S_{AMN}-S_{CBN}=S_{ABC}-\dfrac{1}{3}S_{ABC}-\dfrac{1}{3}S_{ABC}=\dfrac{1}{3}S_{ABC}\)
\(\Rightarrow\dfrac{S_{ABC}}{S_{BMN}}=3\)