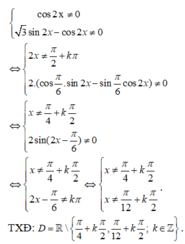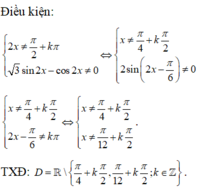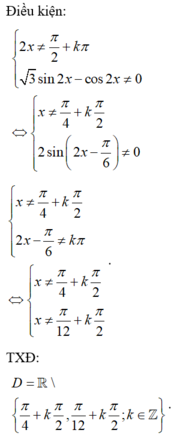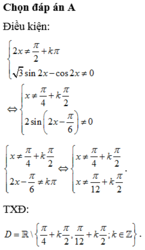tìm tập xác định của hàm số sau: \(\dfrac{1-2sinx}{cos2x}\)

Những câu hỏi liên quan
tìm tập xác định của các hàm số:
1.y=sin2x
2.y=\(\dfrac{1-cosx}{sinx}\)
3.y=\(\dfrac{1-2sinx}{cos2x}\)
4.y=tan\(\left(x+\dfrac{\pi}{4}\right)\)
1. \(D=R\)
2. \(sinx\ne0\Leftrightarrow x\ne k\pi\Rightarrow D=R\backslash\left\{k\pi|k\in R\right\}\)
3. \(cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\Rightarrow D=R\backslash\left\{\dfrac{\pi}{4}+\dfrac{k\pi}{2}|k\in R\right\}\)
4. \(cos\left(x+\dfrac{\pi}{4}\right)\ne0\Leftrightarrow x+\dfrac{\pi}{4}\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+k\pi\Rightarrow D=R\backslash\left\{\dfrac{\pi}{4}+k\pi|k\in R\right\}\)
Đúng 2
Bình luận (1)
tìm tất cả giá trị của m để hàm số sau có tập xác định R
a)y=\(\sqrt{m-cosx}\)
b)y=\(\sqrt{2sinx-m}\)
c)y=\(\dfrac{sinx-1}{cosx+m}\)
a.
\(\Leftrightarrow m-cosx\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge max\left(cosx\right)\)
\(\Leftrightarrow m\ge1\)
b.
\(\Leftrightarrow2sinx-m\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\le2sinx\) ; \(\forall x\)
\(\Leftrightarrow m\le\min\limits_{x\in R}\left(2sinx\right)\)
\(\Leftrightarrow m\le-2\)
c.
\(\Leftrightarrow cosx+m\ne0\) ; \(\forall x\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\max\limits_R\left(cosx\right)\\m< \min\limits_R\left(cosx\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Câu 1: Tìm tập xác định của hàm số y=\(\dfrac{cosx-2}{1-2sinx}\)
Câu2 : Tìm m để hàm số y=\(\sqrt{m-1+2cosx}\) xác đinh trên R
câu3 : Tìm số điểm biểu diễn nghiệm của pt: 2cos5x+1
giúp e với mn ơi
1.
Hàm số xác định khi: \(1-2sinx\ne0\Leftrightarrow sinx\ne\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x\ne\dfrac{\pi}{6}+k2\pi\\x\ne\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
2.
Đặt \(t=cosx\left(t\in\left[-1;1\right]\right)\)
Hàm số xác định trên R khi:
\(m-1+2cosx\ge0\forall x\in R\)
\(\Leftrightarrow m\ge f\left(t\right)=1-2t\forall x\in R\)
\(\Leftrightarrow m\ge maxf\left(t\right)=f\left(-1\right)=3\)
Vậy \(m\ge3\)
Đúng 0
Bình luận (0)
Tìm m để hàm số sau có tập xác định là R
a, \(y=\sqrt{m-5Sinx}\)
b, \(y=\sqrt{2m+Cos2x}\)
c,\(\dfrac{2-Sin3x}{\sqrt{mCosx+1}}\)
a, Vì \(-5sinx\ge-5\Rightarrow m-5sinx\ge0\forall x\Leftrightarrow m\ge5\)
b, Vì \(cos2x\ge-1\Rightarrow2m+cos2x\ge0\forall x\Leftrightarrow2m\ge1\Leftrightarrow m\ge\dfrac{1}{2}\)
c, TH1: \(m=0\) thỏa mãn yêu cầu bài toán
TH2: \(m>0\)
Khi đó: \(-m+1\le mcosx+1\le m+1\)
Yêu cầu bài toán thỏa mãn khi \(-m+1>0\Leftrightarrow m< 1\)
\(\Rightarrow0< m< 1\)
TH3: \(m< 0\)
Khi đó: \(m+1\le mcosx+1\le-m+1\)
Yêu cầu bài toán thỏa mãn khi \(m+1>0\Leftrightarrow m>-1\)
\(\Rightarrow-1< m< 0\)
Vậy \(m\in\left(-1;1\right)\)
Đúng 0
Bình luận (0)
Tìm tập xác định của hàm số sau
y
tan
2
x
3
sin
2
x
-
cos
2
x
Đọc tiếp
Tìm tập xác định của hàm số sau y = tan 2 x 3 sin 2 x - cos 2 x
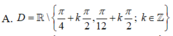
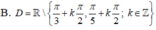
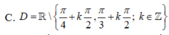
![]()
Tìm tập xác định của hàm số sau
y
tan
2
x
3
sin
2
x
-
cos
2
x
A. B. C. D.
Đọc tiếp
Tìm tập xác định của hàm số sau y = tan 2 x 3 sin 2 x - cos 2 x
A.
![]()
B.
![]()
C.
![]()
D.
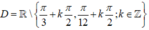
Tìm tập xác định của hàm số sau y
tan
2
x
3
sin
2
x
-
cos
2
x
Đọc tiếp
Tìm tập xác định của hàm số sau y= tan 2 x 3 sin 2 x - cos 2 x
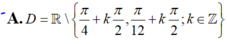
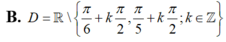
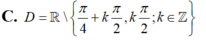
Tìm tập xác định của hàm số sau
y
tan
2
x
3
sin
2
x
-
cos
2
x
A.
D
R
/
...
Đọc tiếp
Tìm tập xác định của hàm số sau y = tan 2 x 3 sin 2 x - cos 2 x
A. D = R / π 4 + k π 2 ; π 12 + k π 2 ; k ∈ Z
B. D = R / π 6 + k π 2 ; π 5 + k π 2 ; k ∈ Z
C. D = R / π 4 + k π 2 ; k π 2 ; k ∈ Z
D. D = R / π 3 + k π 2 ; π 12 + k π 2 ; k ∈ Z
Tìm tập xác định của hàm số sau
y
tan
2
x
3
sin
2
x
-
cos
2
x
A.
D
ℝ
π
4
+
k...
Đọc tiếp
Tìm tập xác định của hàm số sau y = tan 2 x 3 sin 2 x - cos 2 x
A. D = ℝ \ π 4 + k π 2 , π 12 + k π 2 ; k ∈ ℤ
B. D = ℝ \ π 6 + k π 2 , π 5 + k π 2 ; k ∈ ℤ
C. D = ℝ \ π 4 + k π 2 , k π 2 ; k ∈ ℤ
D. D = ℝ \ π 3 + k π 2 , π 12 + k π 2 ; k ∈ ℤ
Chọn A.
Phương pháp: Viết điều kiện và giải.
Cách giải: Điều kiện xác định của hàm số là
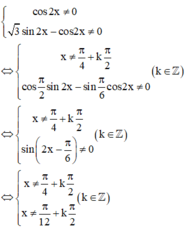
Đúng 0
Bình luận (0)