Chứng minh 1+2=3

Những câu hỏi liên quan
Chứng minh rằng: 1/2!+2/3!+3/4!+......+99/100! <1
Thêm câu này nhé!
Chứng minh rằng: Mọi số nguyên dương thì 3 mũ n+2 - 2 mũ n+2 +3 mũ n -2 mũ n chia hết cho 10
1/3+1/3^2+...+1/3^2016.Chứng minh A nhỏ hơn 1/2
chứng minh rằng: 1/3 + 1/3 mũ 2 + 1/3 mũ 3 + ... + 1/3 mũ 2021<1/2
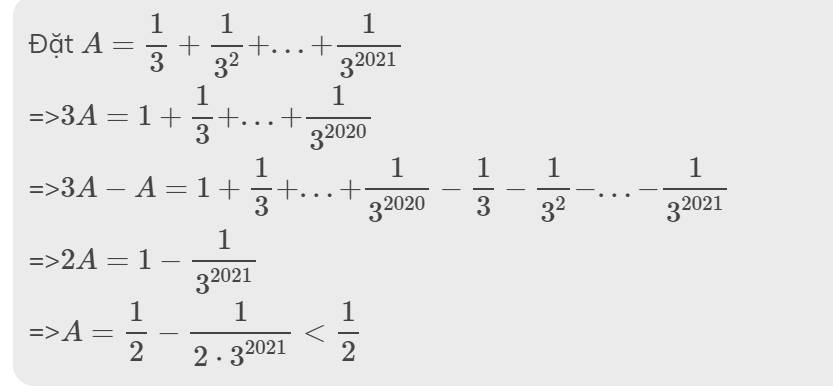
Đặt \(A=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{2021}}\)
=>\(3A=1+\dfrac{1}{3}+...+\dfrac{1}{3^{2020}}\)
=>\(3A-A=1+\dfrac{1}{3}+...+\dfrac{1}{3^{2020}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^{2021}}\)
=>\(2A=1-\dfrac{1}{3^{2021}}\)
=>\(A=\dfrac{1}{2}-\dfrac{1}{2\cdot3^{2021}}< \dfrac{1}{2}\)
Đúng 3
Bình luận (2)
a/ Chứng minh phân số \(\frac{12n+1}{30n+2}\) tối giản
b/ Chứng minh \(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< 1\)
a) Gọi ƯCLN(12n+1;30n+2) = d
\(\Rightarrow\begin{cases}12n+1⋮d\\30n+2⋮d\end{cases}\)
\(\Rightarrow\begin{cases}5\left(12n+1\right)⋮d\\2\left(30n+2\right)⋮d\end{cases}\)
\(\Rightarrow\begin{cases}60n+5⋮d\\60n+4⋮d\end{cases}\)
=> ( 60n + 5 ) - ( 60n + 4 ) \(⋮\) d
=> 1 \(⋮\) d
=> d = 1
Vậy \(\frac{12n+1}{30n+2}\) là phân số tối giản
b) Ta có : \(\frac{1}{2^2}< \frac{1}{1.2}\)
\(\frac{1}{3^2}< \frac{1}{2.3}\)
.........
\(\frac{1}{100^2}< \frac{1}{99.100}\)
=> \(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}\)
Mà \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}< 1\)
\(\Rightarrow\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< 1\) ( đpcm )
Đúng 0
Bình luận (0)
chứng minh rằng: 1/3 + 1/3 mũ 2 + 1/3 mũ 3 + ... + 1/3 mũ 2021
chứng minh A= 1/2!+2/3!+....+2015/2016! <1
Chứng minh rằng :
100 - ( 1 + 1/2 + 1/3 + .....+ 1/100) = 1/2 + 2/3 + 3/4 + .......+ 99/100
Ta có :
\(100-\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{100}\right)\)
\(=100-\left[1+\left(1-\frac{1}{2}\right)+\left(1-\frac{2}{3}\right)+...+\left(1-\frac{99}{100}\right)\right]\)
\(=100-\left[\left(1+1+1+...+1\right)-\left(\frac{1}{2}+\frac{2}{3}+...+\frac{99}{100}\right)\right]\)
\(=100-\left[100-\left(\frac{1}{2}+\frac{2}{3}+...+\frac{99}{100}\right)\right]\)
\(=100-100+\left(\frac{1}{2}+\frac{2}{3}+...+\frac{99}{100}\right)\)
\(=\frac{1}{2}+\frac{2}{3}+...+\frac{99}{100}\)
Đúng 0
Bình luận (0)
ta có 100-(1+1/2+1/3+.....+1/100)
=(1+1+1......1)(99 số 1)-(1+1/2+1/3+......+1/100)
=(1-1)+(1-1/2)+(1-1/3)+.......+(1-1/100)
=1/2+2/3+3/4+.....+99/100
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
chứng minh rằng : 1/2^2+1/3^2+1/4^2+...+1/100^2 < 1
biết a= 1+2^2+2^3+...+2^2019
chứng minh a+1 là số chính phương
@Phí Thị Thanh Duyên không bình luận xúc phạm nha bạn.
Đúng 0
Bình luận (0)