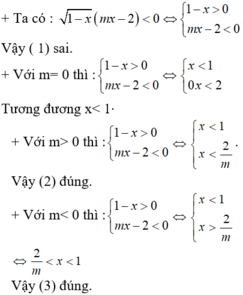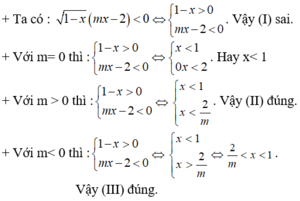giải phương trình: m(mx-1)=x+1

Những câu hỏi liên quan
Cho phương trình x2-mx-1=0
Không giải phương trình CHỨNG MINH rằng với mọi m ta luôn có |x1-x2 |>=2
Ta có x1x2 = -1
=> x1 = -\(\frac{1}{x_2}\)
=> x1 - x2 = x1 + \(\frac{1}{x_1}\)
x1 > 0 thì
x1 + \(\frac{1}{x_1}\) >= 2\(\sqrt{x_1\frac{1}{x_1}}\)= 2
x1 < 0 thì
x1 + \(\frac{1}{x_1}\) <= -2\(\sqrt{x_1\frac{1}{x_1}}\)= -2
Vậy: |x1-x2| >= 2
Đúng 1
Bình luận (0)
Trước khi làm hình như phải cm pt có nghiệm?
( a = 1, b = -m, c = -1)
\(\Delta=b^2-4ac\)
\(=\left(-m\right)^2-4.1.\left(-1\right)\)
\(=m^2+4>0\forall m\)
Vậy pt luôn có 2 nghiệm pb với mọi m
Đúng 0
Bình luận (0)
đenta = m^2 +4 >= 4 >0 với mọi m
=> pt luôn có 2 ng x(1) ; x(2)
theo hệ thức Vi-Et có ; x1 + x2 =m và x1 x2 =-1 (1)
Ta có : |x1 -x2|>=2 <=> (x1 -x2 ) ^2 >=4 <=> x1 ^2 -2x1 x2 + x2 ^2 .=4 <=> (x1 +x2)^2 -4x1 x2 >=4 (2)
thay (2) vào (1) có : m^2 +4 >=4
vì m^2 >=0 Vmọi m => m^2 + 4 >=4 Vmọi m hay |x1 -x2 | >= 2 Vmọi m ==>> dpcm :)
Đúng 0
Bình luận (0)
Giải và biện luận hệ phương trinh ( giải hệ phương trình bằng phương pháp thế )
(1):mx-y=2m
(2):4x-my=m+6
\(\left\{\begin{matrix}mx-y=2m\\4x-my=m+6\end{matrix}\right.\leftrightarrow\left\{\begin{matrix}x=\frac{2m+y}{m}=2+\frac{y}{m}\left(1\right)\\4\left(2+\frac{y}{m}\right)-my=m+6\left(2\right)\end{matrix}\right.\)(đk:m khác 0)
từ (2):\(8+\frac{4y}{m}-my=m+6\leftrightarrow\frac{4y-m^2y}{m}=m-2\)
\(\leftrightarrow y\left(2-m\right)\left(2+m\right)=m\left(m-2\right)\)
Nếu m=2 => 0=0 hệ có vô số nghiệm \(\left\{\begin{matrix}x=\frac{y+4}{2}\\y\in R\end{matrix}\right.\)
Nếu m=-2 => 0=8 , hệ vô nghiệm
Nếu m=0 , hệ có 1 nghiệm \(\left\{\begin{matrix}x=1,5\\y=0\end{matrix}\right.\)
Nếu \(m\ne0;m\ne\pm2\),hệ có 1 nghiệm duy nhất \(\left\{\begin{matrix}x=2+\frac{y}{m}=2-\frac{1}{m+2}=\frac{2m+3}{m+2}\\y=\frac{-m}{m+2}\end{matrix}\right.\)
vậy...
Đúng 0
Bình luận (0)
Cho bất phương trình :
1
-
x
(
m
x
-
2
)
0
(
*
)
Xét các mệnh đề sau: (1) Bất phương trình tương đương với mx - 2 0 (2) m ≥ 0 là điều kiện cần để mọi x 1 là nghiệm của bất phương trình (*) (3) Với m 0 , tập nghiệm của bất phương trình là 2/m x 1 Mệnh...
Đọc tiếp
Cho bất phương trình : 1 - x ( m x - 2 ) < 0 ( * ) Xét các mệnh đề sau:
(1) Bất phương trình tương đương với mx - 2 <0
(2) m ≥ 0 là điều kiện cần để mọi x< 1 là nghiệm của bất phương trình (*)
(3) Với m < 0 , tập nghiệm của bất phương trình là 2/m< x< 1
Mệnh đề nào đúng?
A. Chỉ (1)
B. Chỉ (3)
C. (2) và (3)
D. Tất cả đúng
Cho bất phương trình :
1
-
x
(
mx
-
2
)
0
(
*
)
Xét các mệnh đề sau: (I) Bất phương trình tương đương với mx - 2 0; (II) m ≥ 0 là điều kiện cần để mọi x 1 là nghiệm của bất phương trình (*) (III) Với m 0 , tập nghiệm của bất phương trình là
2...
Đọc tiếp
Cho bất phương trình : 1 - x ( mx - 2 ) < 0 ( * )
Xét các mệnh đề sau:
(I) Bất phương trình tương đương với mx - 2 < 0;
(II) m ≥ 0 là điều kiện cần để mọi x < 1 là nghiệm của bất phương trình (*)
(III) Với m < 0 , tập nghiệm của bất phương trình là 2 m < x < 1
Mệnh đề nào đúng?
A. Chỉ (I)
B. Chỉ (III)
C. (II) và (III)
D. Cả (I), (II), (III)
giải và biện luận phương trình sau
mx-x-m+2=0(m là tham số)
\(mx-x-m+2=0\)
\(\Leftrightarrow mx-x=m-2\)
\(\Leftrightarrow x\left(m-1\right)=m-2\) (1)
Nếu \(m-1\ne0\Leftrightarrow m\ne1\) thì pt(1) có nghiệm duy nhất \(\dfrac{m-2}{m-1}\)
Nếu m = 1 thì pt(1) \(\Leftrightarrow0x=1-2\)
\(\Leftrightarrow0x=-1\) ( vô lý )
⇒ Phương trình vô nghiệm
Kết luận :
+ Nếu \(m\ne1\) thì pt có nghiệm duy nhất \(x=\dfrac{m-2}{m-1}\)
+ Nếu m = 1 thì pt vô nghiệm
Đúng 0
Bình luận (0)
cho Phương trình tử là 2(x-1) mẫu x(x+1) = 1/x
a) tìm điều kiện xác định
b) giải phương trình
\(\frac{2\left(x-1\right)}{x\left(x+1\right)}=\frac{1}{x}\) \(ĐKXĐ:x\ne0;x\ne-1\)
\(\Rightarrow2\left(x-1\right)=\left(x+1\right)\)
\(\Leftrightarrow2x-2=x+1\)
\(\Leftrightarrow x=3\left(nhan\right)\)
Vậy \(S=\left\{3\right\}\)
Đúng 0
Bình luận (0)
Cho hệ phương trình x+my=m+1 mx+y=3m-1 Tìm giá trị của m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x+y
cho phương trình: x^2-mx-m+11=0
a,phương trình có 2 nghiệm x1,x2 khi m=8
b,phương trình có 2 nghiệm thỏa mãn x1^2-(m-2)x1+3x2+x1x2=1
Cho phương trình: x2 + (5-m)x + m -4=0
a) giải phương trình với m=1
b) chứng tỏ phương trình luôn có nghiệm với mọi m
c) tìm m đề phương trình có nghiệm này gấp đôi nghiệm kia