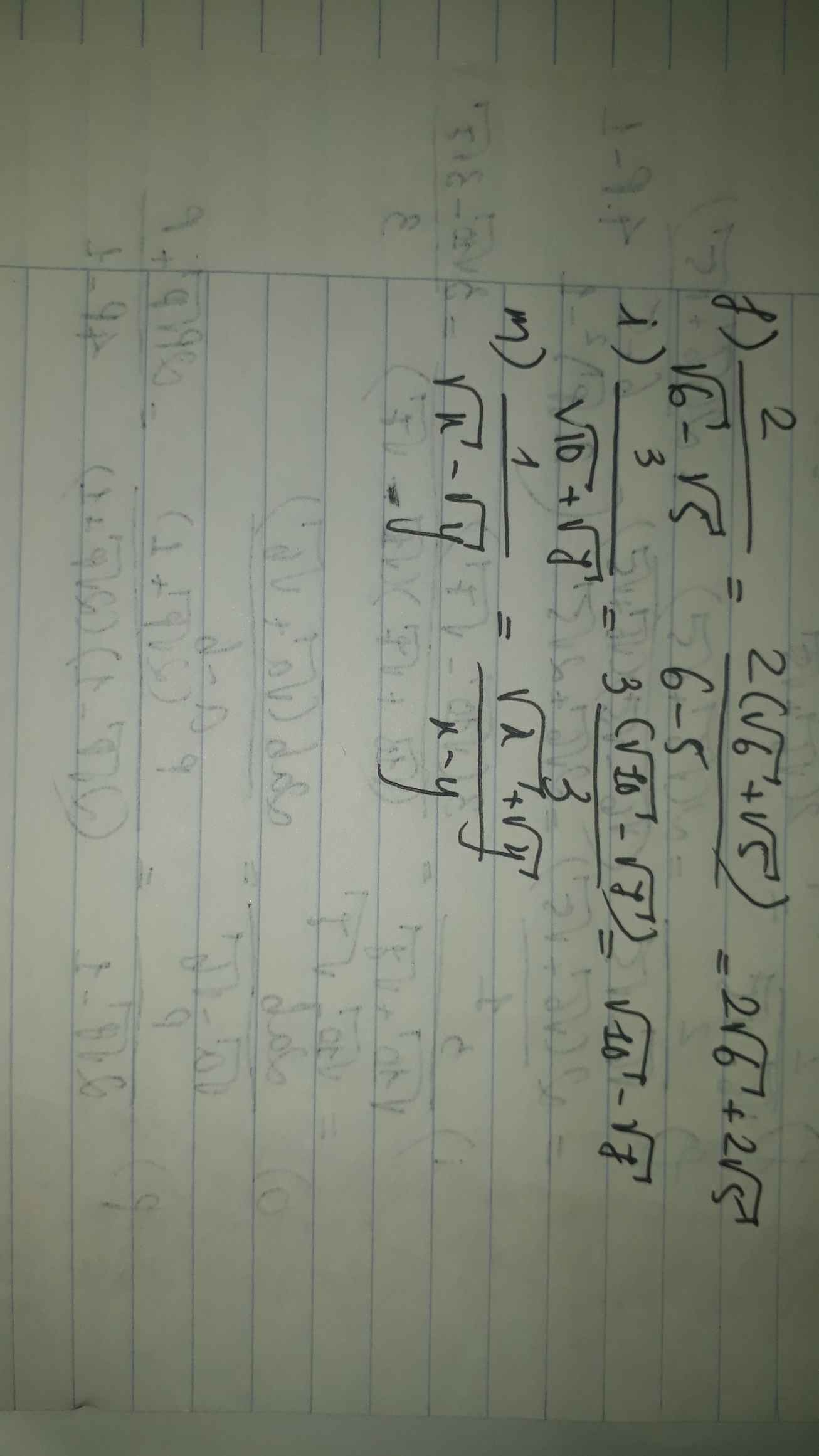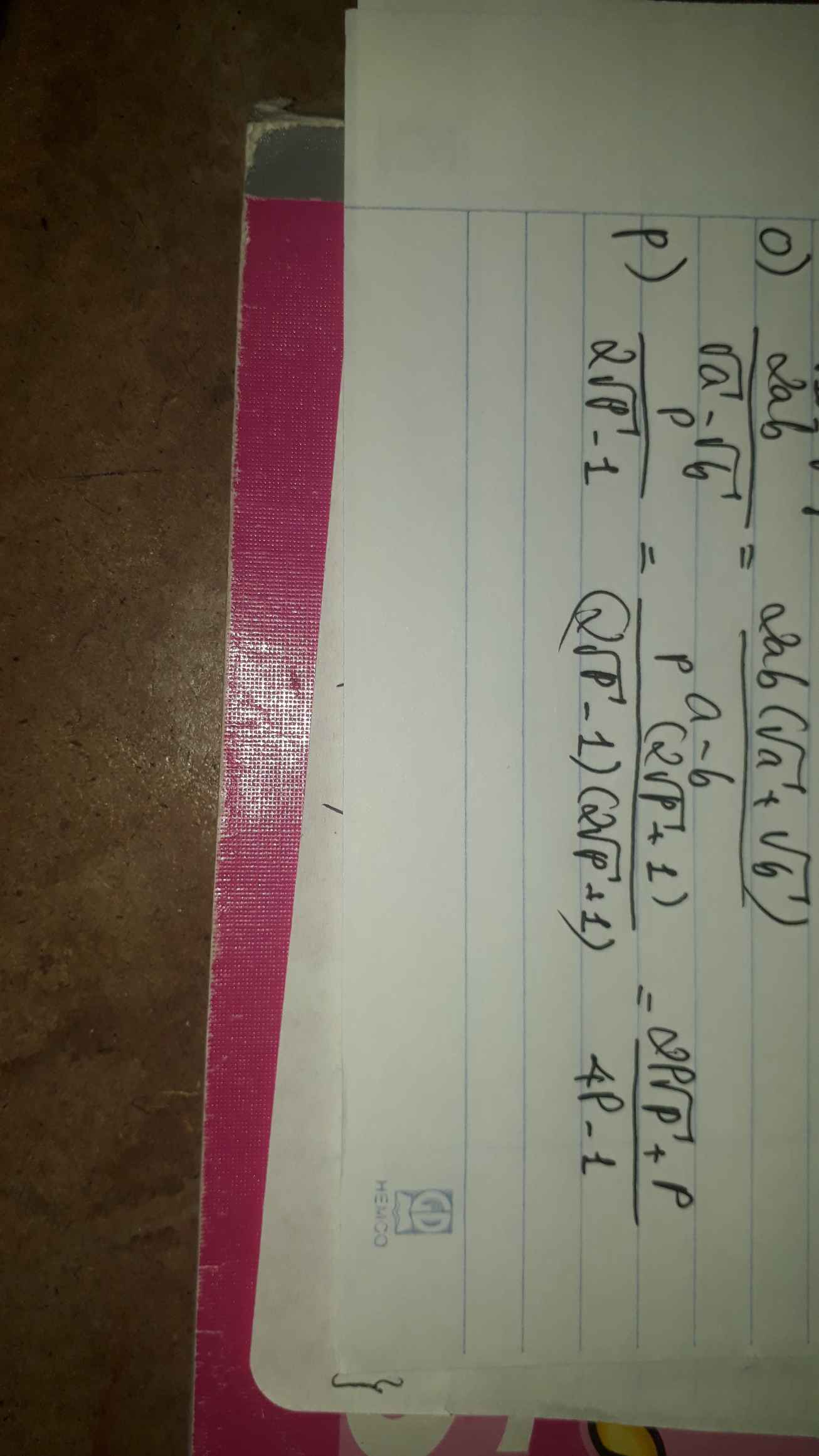Trục căn thức ở mẫu : \(\frac{1}{\sqrt{10}+\sqrt{15}+\sqrt{14}+\sqrt{21}}\)

Những câu hỏi liên quan
TRục căn thức ở mẫu A =\(\frac{1}{\sqrt{2}+\sqrt{3}-\sqrt{6}}\)
\(\frac{\left(\sqrt{2}+\sqrt{3}+\sqrt{6}\right)\left(2\sqrt{6}+1\right)}{23}\)
Đúng 0
Bình luận (0)
\(\sqrt{18}-\frac{1}{3}\sqrt{72}-\sqrt{8}+\frac{2-3\sqrt{2}}{3-\sqrt{2}}\)
Trục căn thức ở mẫu
Ta có: \(\sqrt{18}-\frac{1}{3}\sqrt{72}-\sqrt{8}+\frac{2-3\sqrt{2}}{3-\sqrt{2}}\)
\(=3\sqrt{2}-\frac{6\sqrt{2}}{3}-2\sqrt{2}+\frac{\left(3+\sqrt{2}\right)\left(2-3\sqrt{2}\right)}{9-2}\)
\(=3\sqrt{2}-2\sqrt{2}-2\sqrt{2}-\sqrt{2}\)
\(=-2\sqrt{2}\)
Trục căn thức ở mẫu :
f) \(\dfrac{2}{\sqrt{6}-\sqrt{5}}\)
l) \(\dfrac{3}{\sqrt{10}+\sqrt{7}}\)
m) \(\dfrac{1}{\sqrt{x}-\sqrt{y}}\) (\(x>0;y>0;x\ne y\))
f: \(\dfrac{2}{\sqrt{6}-\sqrt{5}}=2\sqrt{6}+2\sqrt{5}\)
l: \(\dfrac{3}{\sqrt{10}+\sqrt{7}}=\sqrt{10}-\sqrt{7}\)
Đúng 0
Bình luận (0)
Đề : Trục căn thức ở mẫua) dfrac{5}{sqrt{10}} b) dfrac{5}{2sqrt{5}} c) dfrac{1}{3sqrt{20}}d) dfrac{2sqrt{2}+2}{5sqrt{2}} e) dfrac{y+bsqrt{y}}{bsqrt{y}} (với bge0 vàbne0 )
Đọc tiếp
Đề : Trục căn thức ở mẫu
a) \(\dfrac{5}{\sqrt{10}}\) b) \(\dfrac{5}{2\sqrt{5}}\) c) \(\dfrac{1}{3\sqrt{20}}\)
d) \(\dfrac{2\sqrt{2}+2}{5\sqrt{2}}\) e) \(\dfrac{y+b\sqrt{y}}{b\sqrt{y}}\) (với \(b\ge0\) và\(b\ne0\) )
a: \(\dfrac{5}{\sqrt{10}}=\dfrac{5\sqrt{10}}{10}=\dfrac{\sqrt{10}}{2}\)
b: \(\dfrac{5}{2\sqrt{5}}=\dfrac{\sqrt{5}}{2}\)
c: \(\dfrac{1}{3\sqrt{20}}=\dfrac{\sqrt{5}}{30}\)
Đúng 2
Bình luận (0)
a)\(\dfrac{5}{\sqrt{10}}=\dfrac{5\sqrt{10}}{10}=\dfrac{\sqrt{10}}{2}\)
b)\(\dfrac{5}{2\sqrt{5}}=\dfrac{5\sqrt{5}}{2.5}=\dfrac{\sqrt{5}}{2}\)
c)\(\dfrac{1}{3\sqrt{20}}=\dfrac{\sqrt{20}}{3.20}=\dfrac{\sqrt{20}}{60}=\dfrac{\sqrt{5}}{30}\)
Đúng 0
Bình luận (0)
d)\(\dfrac{2\sqrt{2}+2}{5\sqrt{2}}=\dfrac{2.2+2\sqrt{2}}{5.2}=\dfrac{2+\sqrt{2}}{5}\)
e)\(\dfrac{y+b\sqrt{y}}{b\sqrt{y}}=\dfrac{y\sqrt{y}+by}{by}=\dfrac{\sqrt{y}+b}{b}\)
Đúng 0
Bình luận (0)
Đề : Trục căn thức ở mẫuf) dfrac{2}{sqrt{6}-sqrt{5}} l) dfrac{3}{sqrt{10}+sqrt{7}} m) dfrac{1}{sqrt{x}-sqrt{y}} ( x0 ,y0,xne y )o) dfrac{2ab}{sqrt{a}-sqrt{b}} (age0,bge0,ane b) P) dfrac{P}{2sqrt{P}-1} (Pge0 , Pnedfrac{1}{4})
Đọc tiếp
Đề : Trục căn thức ở mẫu
f) \(\dfrac{2}{\sqrt{6}-\sqrt{5}}\) l) \(\dfrac{3}{\sqrt{10}+\sqrt{7}}\) m) \(\dfrac{1}{\sqrt{x}-\sqrt{y}}\) ( x>0 ,y>0,\(x\ne y\) )
o) \(\dfrac{2ab}{\sqrt{a}-\sqrt{b}}\) (\(a\ge0,b\ge0,a\ne b\))
P) \(\dfrac{P}{2\sqrt{P}-1}\) (\(P\ge0\) , \(P\ne\dfrac{1}{4}\))
f: \(\dfrac{2}{\sqrt{6}-\sqrt{5}}=2\sqrt{6}+2\sqrt{5}\)
l: \(\dfrac{3}{\sqrt{10}+\sqrt{7}}=\sqrt{10}-\sqrt{7}\)
m: \(\dfrac{1}{\sqrt{x}-\sqrt{y}}=\dfrac{\sqrt{x}+\sqrt{y}}{x-y}\)
Đúng 1
Bình luận (0)
trục căn ở mẫu các biểu thức \(\frac{5}{\sqrt{5}}\); \(\frac{5}{2+\sqrt{3}}\)
Ta có:
\(\frac{5}{\sqrt{5}}=\frac{5.\sqrt{5}}{5}=\sqrt{5}\)
\(\frac{5}{2+\sqrt{3}}=\frac{5\left(2-\sqrt{3}\right)}{4-3}=\frac{10-5\sqrt{3}}{1}=10-5\sqrt{3}\)
Hok tốt nha
Đúng 0
Bình luận (0)
\(\frac{5}{\sqrt{5}}=\frac{5\sqrt{5}}{\sqrt{5}.\sqrt{5}}\frac{5\sqrt{5}}{5}=\sqrt{5}\)
Đúng 0
Bình luận (0)
\(\frac{5}{2+\sqrt{3}}=\frac{5\left(2-\sqrt{3}\right)}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}=\frac{5\left(2-\sqrt{3}\right)}{4-3}=5\left(2-\sqrt{3}\right)\)
Đúng 0
Bình luận (0)
\(\frac{\sqrt{x}-\sqrt{4y}}{\sqrt{x}+\sqrt{y}}+\frac{3x}{x+\sqrt{xy}}\)
trục căn thức
\(=\frac{\left(\sqrt{x}-\sqrt{4y}\right)\left(\sqrt{x}-\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right).\left(\sqrt{x}-\sqrt{y}\right)}+\frac{3x.\left(x-\sqrt{xy}\right)}{\left(x+\sqrt{xy}\right).\left(x-\sqrt{xy}\right)}\)
\(=\frac{\left(\sqrt{x}-2.\sqrt{y}\right).\left(\sqrt{x}-\sqrt{y}\right)}{x-y}+\frac{3x.\sqrt{x}.\left(\sqrt{x}-\sqrt{y}\right)}{x^2-xy}\)
\(=\frac{\left(\sqrt{x}-2.\sqrt{y}\right).\left(\sqrt{x}-\sqrt{y}\right)}{x-y}+\frac{3x\sqrt{x}.\left(\sqrt{x}-\sqrt{y}\right)}{x.\left(x-y\right)}\)
\(=\frac{\left(\sqrt{x}-2.\sqrt{y}\right).\left(\sqrt{x}-\sqrt{y}\right)}{x-y}+\frac{3\sqrt{x}.\left(\sqrt{x}-\sqrt{y}\right)}{x-y}\)
\(=\frac{\left(\sqrt{x}-2.\sqrt{y}\right).\left(\sqrt{x}-\sqrt{y}\right)+3.\sqrt{x}.\left(\sqrt{x}-\sqrt{y}\right)}{x-y}\)
\(=\frac{\left(\sqrt{x}-\sqrt{y}\right).\left(\sqrt{x}-2.\sqrt{y}+3.\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right).\left(\sqrt{x}+\sqrt{y}\right)}\)
\(=\frac{\left(\sqrt{x}-\sqrt{y}\right).\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right).\left(\sqrt{x}+\sqrt{y}\right)}\)
\(=1\)
Đúng 0
Bình luận (0)
A=\(\frac{1}{\sqrt{2}+\sqrt[3]{4}}\)
Trục căn thức của biểu thức đã cho trên.
Dạng 3.Chứng minh đẳng thức
Bài 1: CM
a)\(\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4-\sqrt{15}}=2\)
b)\(\left(5+\sqrt{21}\right)\left(\sqrt{14}-\sqrt{6}\right)\sqrt{5-\sqrt{21}}=8\)
Bài 2 :CM
\(\dfrac{\sqrt{\sqrt{5}+2}+\sqrt{\sqrt{5}-2}}{\sqrt{2}}=\sqrt{\sqrt{5}+1}\)
Bài 1
a) Đặt VT = A
<=> \(2\sqrt{2}A=\left(8+2\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\sqrt{8-2\sqrt{15}}\)
<=> \(2\sqrt{2}A=\left(\sqrt{5}+\sqrt{3}\right)^2.\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right).\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\)
<=> \(2A=\left(\sqrt{5}+\sqrt{3}\right)^2.\left(\sqrt{5}-\sqrt{3}\right)^2\)
<=> 2A = \(\left(5-3\right)^2=4\)
<=> A = 2
b) Đặt VT = B
<=> \(2\sqrt{2}B=\left(10+2\sqrt{21}\right).\left(\sqrt{14}-\sqrt{6}\right)\sqrt{10-2\sqrt{21}}\)
<=> \(2\sqrt{2}B=\left(\sqrt{7}+\sqrt{3}\right)^2.\sqrt{2}\left(\sqrt{7}-\sqrt{3}\right).\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}\)
<=> \(2B=\left(\sqrt{7}+\sqrt{3}\right)^2.\left(\sqrt{7}-\sqrt{3}\right)^2=\left(7-3\right)^2=16\)
<=> B = 8
Bài 2
Đặt VT = A
<=> A2 = \(\dfrac{\sqrt{5}+2+\sqrt{5}-2+2\sqrt{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}}{2}\)
<=> A2 = \(\dfrac{2\sqrt{5}+2\sqrt{5-4}}{2}=\dfrac{2\sqrt{5}+2}{2}=\sqrt{5}+1\)
<=> \(A=\sqrt{\sqrt{5}+1}\)
Đúng 0
Bình luận (0)