nêu chi tiết phương pháp giải và biện luận hệ phương trình lớp 9
giải và biện luận phương trình \(x^2-2\left(m+1\right)x+2m+10=10\) (hộ e với chi tiết càng tốt ạ)
\(x^2-2\left(m+1\right)x+2m+10=10\)
\(\Leftrightarrow x^2-\left(2m+2\right)x+2m=0\)
\(\text{Δ}=\left(2m+2\right)^2-4\cdot2m=4m^2+8m+4-8m=4m^2+4>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
\(\Delta'=\left(m+1\right)^2-\left(2m+10\right)=m^2-9\)
- Với \(m^2-9< 0\Leftrightarrow-3< m< 3\) pt vô nghiệm
- Với \(m^2-9=0\Rightarrow\left[{}\begin{matrix}m=3\\m=-3\end{matrix}\right.\) pt có nghiệm kép tương ứng \(\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
- Với \(m^2-9>0\Rightarrow\left[{}\begin{matrix}m>3\\m< -3\end{matrix}\right.\) pt có 2 nghiệm pb:
\(\left\{{}\begin{matrix}x_1=m+1-\sqrt{m^2-9}\\x_2=m+1+\sqrt{m^2-9}\end{matrix}\right.\)
Giải và biện luận phương trình bậc 2 bằng phương pháp toán học. Hãy viết chương trình.
#include <bits/stdc++.h>
using namespace std;
double a,b,c,delta,x1,x2;
int main()
{
//freopen("PTB2.inp","r",stdin);
//freopen("PTB2.out","w",stdout);
cin>>a>>b>>c;
delta=(b*b-4*a*c);
if (delta<0) cout<<"-1";
if (delta==0) cout<<fixed<<setprecision(5)<<(-b/(2*a));
if (delta>0)
{
x1=(-b-sqrt(delta))/(2*a);
x2=(-b+sqrt(delta))/(2*a);
cout<<fixed<<setprecision(5)<<x1<<" "<<fixed<<setprecision(5)<<x2;
}
return 0;
}
Giải và biện luận theo tham số m các hệ phương trình sau:
a) 2mx+3y=5(1)
(m+1)x+y=2(2)
Trước (1) và (2) có dấu ngoặc nha. Giải chi tiết giùm mình nha mình tick cho
trình bày phương pháp luận biện chứng và phương pháp luận siêu hình
REFER
Phương pháp biện chứng là phương pháp nhận thức thế giới với quan điểm cơ bản cho rằng, sự tồn tại của mọi sự vật và hiện tượng của thế giới khách quan nói chung đều ở trong những mối liên hệ, trong sự vận động và phát triển theo những quy luật khách quan vốn có của nó.
Phương pháp siêu hình là phương pháp nhận thức thế giới với quan điểm cơ bản cho rằng, mọi sự vật và hiện tượng của thế giới vật chất đều tồn tại cô lập lẫn nhau, cái này ở bên cạnh cái kia và nó luôn ở trong trạng thái tĩnh không có sự vận động và phát triển. Nhưng nếu như có thừa nhận sự phát triển thì chẳng qua chỉ là một quá trình tăng hoặc giảm về số lượng. Mặt khác, quan điểm này không thừa nhận mâu thuẫn bên trong bản thân các sự vật và hiện tượng.
Tham khảo#
Phương pháp luận biện chứng và phương pháp luận siêu hình
- Phương pháp luận là học thuyết về phương pháp nhận thức khoa học và cải tạo thế giới
- Phương pháp luận có 2 loại:
+ Phương pháp luận biện chứng: xem xét sự vật, hiện tượng trong sự ràng buộc lẫn nhau giữa chúng trong sự vận động và phát triển không ngừng của chúng
Các câu nói có yếu tố biện chứng: các câu thành ngữ, tục ngữ (Rút dây động rừng, Tre già măng mọc, Môi hở răng lạnh, Nước chảy đá mòn,), Không ai tắm hai lần trên cùng một dòng sông,
+ Phương pháp luận siêu hình: xem xét sự vật, hiện tượng một cách phiến diện, chỉ thấy chúng tồn tại trong trạng thái cô lập, không vận động, không phát triển, áp dụng một cách máy móc đặc tính của sự vật này vào sự vật khác
Vd: Do không nắm được đặc tính riêng của giới hữu cơ, ông đã cho rằng, cơ thể con người cũng giống như các bộ phận của một cỗ máy , quan niệm thầy bói trong chuyện thầy bói xem voi, Đèn nhà ai nhà nấy rạng,
tham khảo
Phương pháp siêu hình làm cho con người “chỉ nhìn thấy những sự vật riêng biệt mà không nhìn thấy mối liên hệ qua lại giữa những sự vật ấy, chỉ nhìn thấy sự tồn tại của những sự vật ấy mà không nhìn thấy sự phát sinh và sự tiêu vong của những sự vật ấy, chỉ nhìn thấy trạng thái tĩnh của những sự vật ấy mà quên mất sự ...
Cho hệ phương trình: { 2mx + y = 2 (m mà than số)
{ 8x + my = m + 2
a) Giải hệ phương trình khi m = -1
b) Tìm m để hệ phương trình có nghiệm là x = 2; y = 6
c) Giải và biện luận hệ phương trình theo m
d) Trong trường hợp có nghiệm duy nhất:
+ Tìm hệ thức liên hệ giữa 2 nghiệm không phụ thuộc m
+ Tìm m để 4x + 3y = 7
+ Tìm m để x - y > 0
+ Tìm m để P = y^2 - 2x đạt giá trị nhỏ nhất
Cho hệ phương trình \(|^{mx+2y=1}_{3x+\left(m+1\right)y=-1}\) (với m là tham số)
a) Giải hệ phương trình với m = 3.
b) Giải và biện luận hệ phương trình theo m.
c) Tìm m để hệ phương trình có nghiệm là số nguyên.
Giải và biện luận theo tham số m hệ phương trình:
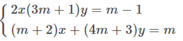
Nhân phương trình thứ nhất của hệ với m + 2, nhân phương trình thứ hai với 2 ta được hệ phương trình
![]()
Trừ hai phương trình vế theo vế ta được phương trình:
(3m2 - m - 4)y = (m + 1)(m + 2) (1)
+ Với m = -1 phương trình (1) có dạng: 0y = 0
Phương trình này nhận mọi giá trị thức của y làm nghiệm. Lúc đó thay m = -1 vào hệ phương trình đã cho, hai phương trình trở thành một phương trình.
x - y = 1 ⇒ y = x + 1, x tùy ý.
+ Với m = 4/3 phương trình (1) có dạng: 0y = -14/9
Phương trình này vô nghiệm, do đó hệ phương trình đã cho vô nghiệm.
+ Với m ≠ -1 và m ≠ 4/3, phương trình (1) có nghiệm duy nhất
![]()
Thay vào một trong hai phương trình của hệ đã cho ta suy ra
![]()
Kết luận
m = 4/3: Hệ phương trình đã cho vô nghiệm.
m = -1: Hệ phương trình đã cho có vô số nghiệm
x = a, y = a + 1, a là số thực tùy ý.
m ≠ 1, m ≠ 4/3: Hệ phương trình đã cho có nghiệm duy nhất :
![]()
Giải giúp em với ạ:
Cho hệ phương trình: mx + 4y = 10 - m và x + my = 4 (m là tham số)
a, giải hệ phương trình khi m = √2
b, giải và biện luận hệ phương trình theo m
Cô làm câu b thôi nhé :)
Ta có hệ \(\hept{\begin{cases}mx+4y=10-m\\x+my=4\end{cases}}\Leftrightarrow\hept{\begin{cases}m\left(4-my\right)+4y=10-m\\x=4-my\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(4-m^2\right)y=10-5m\left(1\right)\\x=4-my\end{cases}}\)
Với \(4-m^2=0\Leftrightarrow m=2\) hoặc \(m=-2\)
Xét m =2, phương trình (1) tương đương 0.x = 0. Vậy hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
Xét m = -2, phương trình (1) tương đương 0.x = 20. Vậy hệ phương trình vô nghiệm.
Với \(4-m^2\ne0\Leftrightarrow m\ne2\) và \(m\ne-2\), phương trình (1) tương đương \(y=\frac{10-5m}{4-m^2}=\frac{5}{2+m}\)
Từ đó : \(x=\frac{8-m}{2+m}\)
Kết luận:
+ m = 2, hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
+ m = - 2, hệ phương trình vô nghiệm.
+ \(m\ne2;m\ne-2\) hệ có 1 nghiệm duy nhất \(\hept{\begin{cases}x=\frac{8-m}{2+m}\\y=\frac{5}{2+m}\end{cases}}\)
Chúc em học tập tốt :)

hehe
Hỏi từ lâu nhưng bây giờ em trả lời lại cho vui
Giải và biện luận hệ phương trình
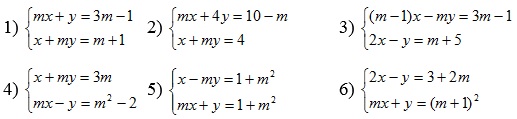
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????/