cho tam giác ABC trên AB AC lần lượt lấy M N chứng minh SAMN/SABC=AM/AB.AN/AC

Những câu hỏi liên quan
Cho tam giác ABC . Trên AB lấy M sao cho AM =1/3 AB . Trên AC lấy N sao cho AN=1/2 AC . Biết SAMN = 15 cm vuông . Tìm SABC?
Cho tam giác ABC, điểm M nằm trên AB sao cho AM =
MB. Điểm N nằm trên AC sao cho AN = 1/3 AC. Biết SAMN = 6cm2. Tính SABC
cứu minhfhhhhhhhhh huhu
Lời giải:
$\frac{S_{AMN}}{S_{ANB}}=\frac{AM}{AB}=\frac{1}{2}$
Suy ra $S_{AMN}=\frac{1}{2}\times S_{ANB}$
$\frac{S_{ABN}}{S_{ABC}}=\frac{AN}{AC}=\frac{1}{3}$
$\Rightarrow S_{ABN}=\frac{1}{3}S_{ABC}$
Suy ra $S_{AMN}=\frac{1}{2}\times \frac{1}{3}\times S_{ABC}$
$\Rightarrow 6=\frac{1}{6}\times S_{ABC}$
$\Rightarrow S_{ABC}=36$ (cm2)
Đúng 0
Bình luận (0)
| Cho tam giác ABC. Lấy điểm M trên AB, N trên AC và P trên BC sao cho AM = 2 BM, CN = 2 AN và CP = 2 BP. AM cắt MN tại Q. Biết SAMQ = 12 cm2. Tính SABQ, SACQ, SAQN, SAMN, SABC, SABP, SCNQP |
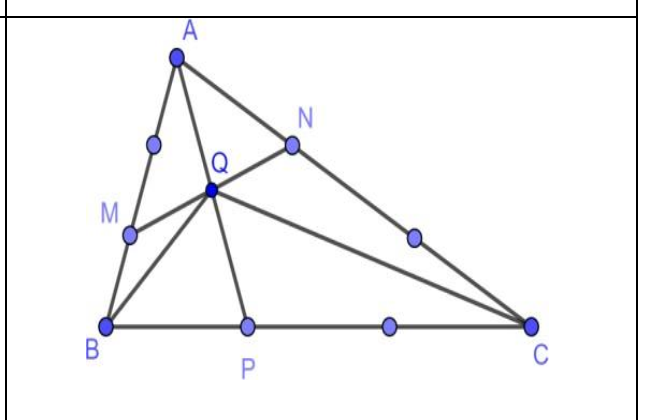
AM=2BM
=>AM/AB=2/3
=>S AMQ/S ABQ=2/3
=>S ABQ=18cm2
Lấy K,E lần lượt trên CA,CB sao cho CK=1/3CA; CE=1/3CB
=>AN=NK=KC và BP=PE=EC
Xét ΔCAB có CP/CB=CN/CA=2/3
nên PN//AB và PN/AB=2/3
=>PN//AM và PN=AM
=>AMPN là hình bình hành
=>Q là trung điểm chung của AP và MN
S ABQ=18cm2
=>S ABP=2*18=36cm2
Q là trung điểm của MN
=>S AMQ=S AQN=12cm2
=>S AQC=36cm2
S AMN=12+12=24cm2
BP=1/3BC
=>S ABC=3*36=108cm2
Đúng 0
Bình luận (0)
Nhanh nha mọi người.
Làm cách lớp 5, phải đúng.
Cảm ơn nhìu!!!
Cho xin lời giải ạ.❄
Bài 5: Cho tam giác ABC. Trên AB lấy điểm M sao cho AM=AB, trên AC lấy
điểm N sao cho AN= AC.
a) So sánh SAMN và SABC?
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh AC lấy điểm D sao cho AB = AD. Trên tia đối của tia AB lấy điểm E sao cho AC = AE a) chứng minh tam giác ABC = tam giác ADE b) gọi M , N lần lượt là trung điểm của BC và DE , chứng minh AM = AN c) tính số đo của góc MAN
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
Đúng 0
Bình luận (0)
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: AM=ED/2
AN=BC/2
mà ED=BC
nên AM=AN
Đúng 0
Bình luận (0)
cho tam giác ABC, trên tia đối tia AB lấy điểm M sao cho AB=AM. Trên tia AC lấy điểm N sao cho AC=AN. Chứng minh:
a) tam giác ABC=tam giác AMN
b) chứng minh BC//MN
c) gọi P và Q lần lượt là trung điểm của BC và MN. Chứng minh A là trung điểm của PQ
Cho tam giác ABC vuông tại A , đường cao AH.
a) Chứng minh : tam giác ABC đồng dạng với tam giác HAC.
b) Biết AB = 6 cm , AC = 8 cm.Tính độ dài các cạnh BC , AH, CH , BH.
c) Trên AH lấy điểm M sao cho AM= 1,2 cm , từ điểm M kẻ đường thẳng song song với BC lần lượt cagws AB và AC tại E và F. Tính Saef phần Sabc, Sabc , Saef.
a) Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat{BAC}=\widehat{AHC}=90^0\)
\(\widehat{ABC}=\widehat{HAC}\) do cùng phụ với góc BAH )
suy ra: \(\Delta ABC~\Delta HAC\)
b) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)
Áp dụng hệ thức lượng ta có:
\(AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8\)cm
\(CH=\frac{AC^2}{BC}=\frac{8^2}{10}=6,4\)cm
\(BH=BC-HC=10-6,4=3,6\)cm
Đúng 1
Bình luận (0)
cho tgiac ABC cân tại A lấy điểm M,N lần lượt trên cạnh AB và AC sao cho AM=AN
a) chứng minh MN//BC
b)Chứng minh BM=CN
c) cminh Tam giác AMN = Tam giác CNM
a: Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
b: AM+MB=AB
AN+NC=AC
mà AM=AN và AB=AC
nên MB=NC
c: Đề sai rồi bạn
Đúng 0
Bình luận (0)
Cho Tam giác ABC có AB = 4cm, AC = 6cm. Trên cạnh AB và AC lần lượt lấy điểm M và N sao cho AM =1cm, AN = 1,5cm. a) Chứng minh MN // BC b) Biết MP // AC, chứng minh Tam giác AMN đồng dạng với Tam giác MBP. c) Tìm tỉ số diện tích của Tam giác AMP và Tam giác ACP. MÌNH CHỦ YẾU CẦN CÂU C NHA
a) Ta có: \(\dfrac{AM}{AB}=\dfrac{1}{4}\)
\(\dfrac{AN}{AC}=\dfrac{1.5}{6}=\dfrac{1}{4}\)
Do đó: \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)\(\left(=\dfrac{1}{4}\right)\)
Xét ΔABC có
M\(\in\)AB(gt)
N\(\in\)AC(gt)
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)(cmt)
Do đó: MN//BC(Định lí Ta lét đảo)
Đúng 0
Bình luận (0)
















