Cho tam giác ABC vuông tại A, AB= 6 cm, AC=8 cm, đường phân giác AM, đường vuông góc với MC tại M và cắt AC ở E. Chứng minh rằng :
a, Tam giác ABC đồng dạng với tam giác MEC
b, Tính BC và BM
c, Tính diện tích tam giác ABC và diện tích ABME
Cho tam giác ABC vuông tại A có AB = 6 cm, AC= 8 cm, đường trung tuyến M. Gọi d là đường thẳng vuông góc với AM tại A. Kể BD vuông góc với d tại D, kẻ CE vuông góc với d tại E. a, Chứng minh: tam giác ABC đồng dạng với tam giác CAE. b, Tính CE
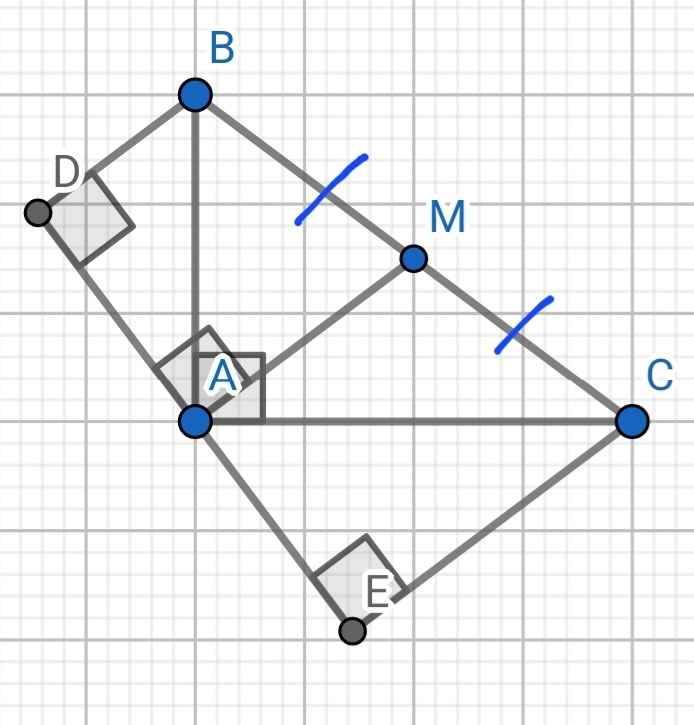
a) Sửa đề: Chứng minh ∆ABC ∽ ∆EAC
Giải:
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
= 10 : 2 = 5 (cm)
∆AMC có AM = CM = 5 (cm)
⇒ ∆AMC cân tại M
⇒ ∠MAC = ∠MCA (hai góc ở đáy)
Do MA ⊥ DE (gt)
CE ⊥ DE (gt)
⇒ MA // DE
⇒ ∠MAC = ∠ACE (so le trong)
Mà ∠MAC = ∠MCA (cmt)
⇒ ∠MAC = ∠ACE
⇒ ∠ACE = ∠BCA (do ∠MAC = ∠BAC)
Xét hai tam giác vuông:
∆ABC và ∆EAC có:
∠BCA = ∠ACE (cmt)
⇒ ∆ABC ∽ ∆EAC (g-g)
b) Do ∆ABC ∽ ∆EAC (cmt)
⇒ AC/CE = BC/AC
⇒ CE = AC²/BC
= 8²/10
= 6,4 (cm)
a) Xét tam giác BHA và tam giác BAC có
góc BHA= góc BAC (=90)
góc B chung
=> tam giác BHA đồng dạng tam giác BAC (g.g)
cho tam giác abc vuông tại A AB=6 cm AC=8 cm Vẽ đường cao AH
a,Chứng minh tam giác AHB đồng dạng với tam giác CAB
b,TÍnh độ dài AH và HB
c,Lấy điểm D bất kì trên cạnh AC Kẻ đường thẳng vuông góc với HD tại H cắt AB tại E Chứng minh tam giác BHE đồng dạng với tam giác AHD,góc BAH=góc EDH
d,Khi D là trung điểm AC tính diện tích tam giác HDE
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Ta có: ΔAHB\(\sim\)ΔCAB(cmt)
nên \(\dfrac{AH}{CA}=\dfrac{HB}{AB}=\dfrac{AB}{CB}\)(Các cặp cạnh tương ứng tỉ lệ)
\(\Leftrightarrow\dfrac{AH}{8}=\dfrac{HB}{6}=\dfrac{6}{10}=\dfrac{3}{5}\)
Suy ra: \(\left\{{}\begin{matrix}\dfrac{AH}{8}=\dfrac{3}{5}\\\dfrac{HB}{6}=\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=4.8\left(cm\right)\\HB=3.6\left(cm\right)\end{matrix}\right.\)
Vậy: AH=4,8cm; HB=3,6cm
a) Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔAHB\(\sim\)ΔCAB(g-g)
cho tam giác abc cân tại a (ab<ac) và d là trung điểm của bc. từ d vẽ đường thẳng vuông góc với bc cắt ac tại e.
a) cm tam giác dec đồng dạng với tam giác abc
b) đường vuông góc với bc kẻ từ b cắt ca tại f. cm bf^2=fa.fc
c) gọi I là trung điểm của ab. chứng minh tam giác fib đồng dạng với tam giác fdc
d) hai đường thẳng fi và ed giao tại m. chứng minh mc vuông góc với fc
cho tam giác abc cân tại a (ab<ac) và d là trung điểm của bc. từ d vẽ đường thẳng vuông góc với bc cắt ac tại e.
a) cm tam giác dec đồng dạng với tam giác abc
b) đường vuông góc với bc kẻ từ b cắt ca tại f. cm bf^2=fa.fc
c) gọi I là trung điểm của ab. chứng minh tam giác fib đồng dạng với tam giác fdc
d) hai đường thẳng fi và ed giao tại m. chứng minh mc vuông góc với fc
Cho tam giác ABC vuông tại A có AB=15 cm AC=20cm. Vẽ AH vuông góc với BC tại H.
1,Chứng minh tam giác HBA và tam giác ABC đồng dạng.
2,Tính BC, AH.
3,Vẽ tia phân giác của góc BAH cắt BH tại D. Tính BH DH .
4, Trên cạnh HC lấy E sao cho HE =HA, qua E vẽ đường thẳng vuông góc với cạnh BC cắt AC tại M, qua C vẽ đường thẳng vuông góc với BC cắt tia phân giác của góc MEC tại F. Chứng minh H,M,F thẳng hàng
cho tam giác ABC vuông tại A biết AB=3cm,AC=4cm.Gọi M là trung điểm của BC.Qua M kẻ đường thẳng vuông góc với Bc tại M CẮT AC,AB lần lượt ở E và F
a)chứng minh: tam giác MEC đồng dạng tam giác ABC.Tính ME
b)chứng minh: ME.EF=AE.CE
c)BE cắt FC ở K .Chứng minh AC là phân giác của góc MAK
a: Xét ΔMEC vuông tại M và ΔABC vuông tại A có
góc C chung
=>ΔMEC đồng dạng với ΔABC
=>ME/AB=MC/AC
=>ME/3=2,5/4=5/8
=>ME=15/8cm
b: Xét ΔEAF vuông tại A và ΔEMC vuông tại M có
góc AEF=góc MEC
=>ΔEAF đồng dạng với ΔEMC
=>EA/EM=EF/EC
=>EA*EC=EF*EM
Cho tam giác ABC có AB=3cm , AC=4cm, BC=5cm.Đường phân giác góc A cắt BC tại D.Qua D vẽ đường vuông góc với BC cắt AC tại E và BA tại K.
a) CM tam giác ABC vuông
b) tính DB, DC
c) CM tam giác EDC đồng dạng tam giác BDK
d)chứng minh DE=DB
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔACB có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{10}{7}\)
Do đó:BD=30/7cm; CD=40/7cm
Cho tam giác ABC có AB=3cm , AC=4cm, BC=5cm.Đường phân giác góc A cắt BC tại D.Qua D vẽ đường vuông góc với BC cắt AC tại E và BA tại K.
a) CM tam giác ABC vuông
b) tính DB, DC
c) CM tam giác EDC đồng dạng tam giác BDK
d)chứng minh DE=DB
a) Ta có: \(BC^2=5^2=25\)
\(AB^2+AC^2=3^2+4^2=25\)
Do đó: \(BC^2=AB^2+AC^2\)(=25)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)