x/11=y/12;y/3=z/7 và 2x+y-z=152

Những câu hỏi liên quan
Câu 34: Cho dãy tỉ số bằng nhau 𝑥+1/2=𝑦+5/3=𝑧+12/4 𝑣à 𝑥+𝑦+𝑧=36 thì giá trị của x ,y, z tìm được là
A. x = 11, y = 13, z = 12 B. x = 12, y = 13, z = 11
C. x = 13, y = 11, z = 12 D. x = 12, y = 11, z = 13
y x \(\dfrac{11}{12}\) + y x \(\dfrac{3}{4}\) = \(\dfrac{10}{11}\)
y.(11/12+3/4)=10/11
y.5/3=10/11
y=10/11:5/3
y=6/11
Đúng 0
Bình luận (0)
\(=>y=\dfrac{10}{11}:\left(\dfrac{11}{12}+\dfrac{3}{4}\right)=\dfrac{10}{11}:\left(\dfrac{11}{12}+\dfrac{9}{12}\right)=\dfrac{10}{11}:\dfrac{5}{3}=\dfrac{6}{11}\)
Đúng 0
Bình luận (0)
\(\text{=> }y.\left(\dfrac{11}{12}+\dfrac{3}{4}\right)=\dfrac{10}{11}=>y.\dfrac{5}{3}=\dfrac{10}{11}=>y=\dfrac{10}{11}:\dfrac{5}{3}=\dfrac{6}{11}\)
Đúng 2
Bình luận (0)
Tìm số nguyên x, y biết x-11/y-10 = 11/10 và |x-y| = 12
|x-y|=12
=>x-y=12 hoặc x-y=-12
=>x=y+12 hoặc x=y-12
\(\dfrac{x-11}{y-10}=\dfrac{11}{10}\)
=>10x-110=11y-110
=>10x-11y=0(1)
Trường hợp 1: x=y+12
(1)=> 10(y+12)-11y=0
=>10y+120-11y=0
=>y=120
=>x=132
Trường hợp 2: x=y-12
(1) =>10(y-12)-11y=0
=>y=-120
=>x=-132
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
-
1
2
+
y
+
1
2
+
z
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + y + 1 2 + z 2 = 11 và hai đường thẳng d 1 : x - 5 1 = y + 1 1 = z - 1 2 ; d 2 : x + 1 1 = y 2 = z 1 ; Viết phương trình tất cả các mặt phẳng tiếp xúc với mặt cầu (S) đồng thời song song với hai đường thẳng d 1 , d 2
A. α : 3x-y-z-15=0
B. α : 3x-y-z+7=0
C. α : 3x-y-z-7=0
D. α : 3x-y-z+7 =0 hoặc α : 3x-y-z-15=0
Đáp án B
Mặt cầu S : x - 1 2 + y + 1 2 + z 2 = 11 có tâm I(1;-1;0) bán kính R= 11
Các đường thẳng d 1 , d 2 có vectơ chỉ phương lần lượt là:
![]()
Mặt phẳng α song song với d 1 , d 2 có vectơ pháp tuyến là:
![]()
α có dạng: α : 3x-y-z+d=0. Vì α tiếp xúc với (S ) nên: d(I; α )=R
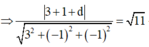
![]()
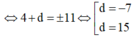
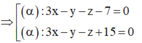
Nhận thấy điểm A(5;-1;1) ∈ d 1 cũng thuộc vào mặt phẳng 3x-y-z+15=0 =>mặt phẳng này chứa d 1
Vậy phương trình mặt phẳng α thỏa mãn yêu cầu bài toán là: α : 3x-y-z+7=0
Đúng 0
Bình luận (0)
x/y=11/7 và x-y=12
x/y = 11/7
x - y = 12
Hiệu số phần bằng nhau :
11 - 7 = 4 ( phần )
x = 12 : 4 . 11 = 33
y = 12 : 4 . 7 = 21
Vậy x/y = 33/21
Đúng 0
Bình luận (0)
áp dụng tính chất dãy tỉ số bằng nhau ta có:x/11=y/7=(x-y)/(11-7)=12/4=3
x/11=3 suy ra x=33
y/7=3 suy ra y=21
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm các số nguyên x,y biết:
a) 3x-2y+xy=17;
b) x-11 / y-10=11/10 và |x-y|=12
Tính các biểu thức sau :
\(\dfrac{a.\left(7\cdot x^2+11\cdot y^2\right)}{\left(14\cdot x^{12}-11\cdot y^2\right)}.\left(\dfrac{x}{11}\right)=\left(\dfrac{y}{7}\right)\)
Chia đa thức cho đơn thức sau: \(\left(3x^{15}y^{16}z^{14}-\frac{2}{7}x^{13}y^{15}z^{11}+x^{12}y^{14}z^{13}\right):\left(\frac{-7}{3}x^{12}y^{14}z^{11}\right)\)
Tìm hai số x và y biết: \(\dfrac{x}{{11}} = \dfrac{y}{{17}}\) và x – y = 12
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\begin{array}{l}\dfrac{x}{{11}} = \dfrac{y}{{17}} = \dfrac{{x - y}}{{11 - 17}} = \dfrac{{12}}{{ - 6}} = - 2\\ \Rightarrow x = ( - 2).11 = - 22\\y = ( - 2).17 = - 34\end{array}\)
Vậy \(x = -22; y = -34\).
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
−
1
2
+
y
+
1
2
+
z
2
11
và hai đường thẳng
d
1
:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 1 2 + y + 1 2 + z 2 = 11 và hai đường thẳng d 1 : x − 5 1 = y + 1 1 = z − 1 2 ; d 2 : x + 1 1 = y 2 = z 1 . Viết phương trình tất cả các mặt phẳng tiếp xúc với mặt cầu (S) đồng thời song song với hai đường thẳng d 1 , d 2
A. α : 3 x − y − z − 15 = 0
B. α : 3 x − y − z + 7 = 0
C. α : 3 x − y − z − 7 = 0
D. α : 3 x − y − z + 7 = 0 hoặc α : 3 x − y − z − 15 = 0


























