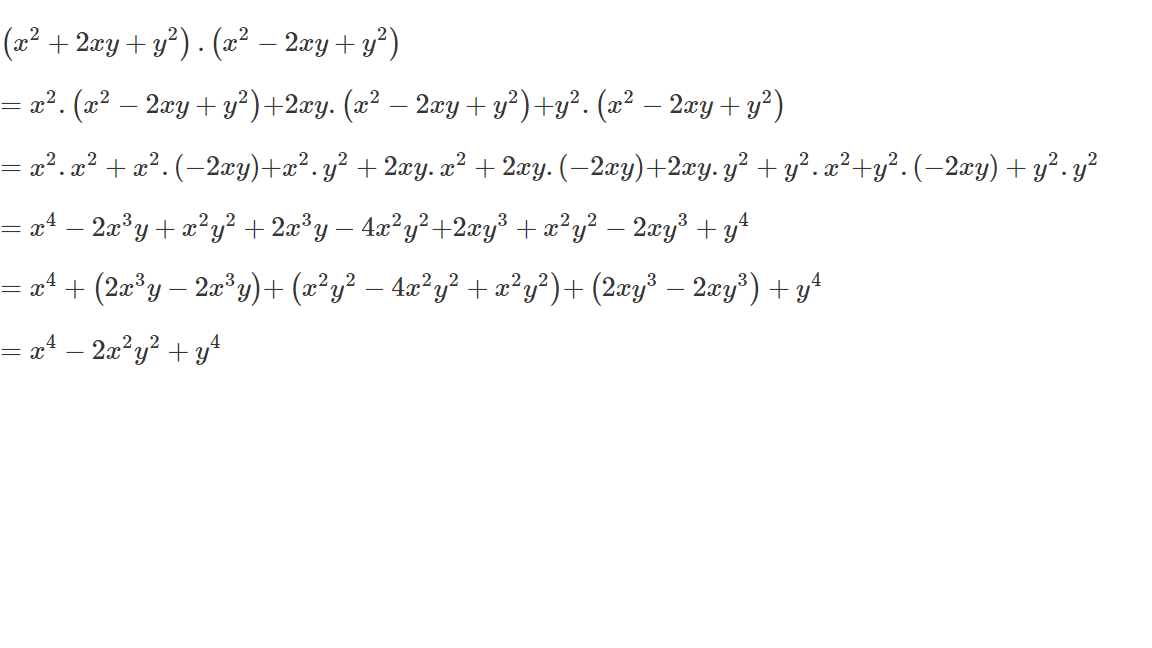Tìm đa thức M sao cho tổng của M với đa thức x2 - 2xy+ y2+x2 là 1 s không chứa biến x

Những câu hỏi liên quan
tìm đa thức M sao cho tổng của M với đa thức x^2-2xy+y^2-2xy+z^2 không chứa biến x
Để tổng của M với đa thức \(x^2-2xy+y^2-2xy+z^2\) không chứa x thì \(M+x^2-2xy+y^2-2xy+z^2=y^2-z^2\)
=>\(M+x^2-4xy=0\)
=>\(M=-x^2+4xy\)
Đúng 0
Bình luận (0)
Tìm một đa thức M sao cho tổng của M vơi đa thức x2-2xy+y2-3xz+z2 không chứa biến X
Có vô số đa thức M như vậy,chẳng hạn \(M=-x^2-2xy+5y^2-3xz+7z^2\)
Thì ta có : \(\left(-x^2-2xy+5y^2-3xz+7z^2\right)+\left(x^2+2xy-y^2+3xz-z^2\right)=4y^2+6z^2\)(đơn thức này không chứa x)
Tìm các đa thức A và B, biết:
a) A + (x2- 4xy2 + 2xz - 3y2 = 0
b) Tổng của đa thức B với đa thức (4x2y + 5y2 - 3xz +z2) là một đa thức không chứa biến x
a) A+(x2-4xy2+2xz-3y2)=0
⇒ A = -x2+4xy2-2xz+3y2
= -2x2+4xy2-2xz
còn câu b mik ko biết đa thức B là gì
Đúng 3
Bình luận (0)
tìm đa thức m sao cho tổng của m với đa thức 3x^4+5x^2y+y4-3xy+z^2 là một đa thức không chứa biến x
Cho hai đa thức:
M = x2 – 2xy + y2;
N = y2 + 2xy + x2 + 1.
Tính M – N.
M – N = (x2 – 2xy + y2)– (y2 +2xy +x2 + 1)
= x2 – 2xy + y2 – y2 – 2xy – x2 – 1
= (x2– x2) + (y2 – y2) + (– 2xy – 2xy) – 1
= 0 + 0 – 4xy – 1
= – 4xy – 1.
Đúng 0
Bình luận (0)
Cho hai đa thức:
M = x2 – 2xy + y2;
N = y2 + 2xy + x2 + 1.
Tính M + N;
M + N = (x2 – 2xy + y2)+ (y2 + 2xy + x2 + 1)
= x2 – 2xy + y2 + y2 + 2xy + x2 + 1
= (x2+ x2) + (y2 + y2) + (– 2xy+ 2xy) + 1
= 2x2 + 2y2 + 0 + 1
= 2x2 + 2y2 +1
Đúng 0
Bình luận (0)
giúp mình với cần gấp toán 7 b1 . cho 2 đa thức M=2m^2-3xy-y^2+(-3x^2+2xy-y^2) tính a M+N b M-N
b2 tìm đa thức M sao cho tổng của M và đa thức x^2y^2-y^3+2xz-z^2 ( không chứa biến x)
tui quên ghi đa thức N của bài 1
N=x^2 - xy +3y^2
Đúng 0
Bình luận (0)
Bạn gì đó ? có facebook không ạ ? kết bạn để dễ nói đi ạ ! fb tui tên Khánh Thư ạ
Đúng 0
Bình luận (0)
Tìm đa thức M sao cho tổng của đa thức M và đa thức \(x^2\)+ 3xy - \(y^2\)+ 2xy - \(z^2\)không chứa biến x
Có vô số đa thức thỏa mãn, tớ lấy 1 đa thức thôi
M=-x2-3xy-2xy
Ngoài ra còn vô số đa thức, bạn có thể lấy 1 đa thức khác nếu muốn
Đúng 0
Bình luận (0)
tích của đa thức : x2+2xy+y2 với đa thức x2-2xy+y2
\(\left(x^2+2xy+y^2\right)\left(x^2-2xy+y^2\right)=\left(x-y\right)^2\cdot\left(x+y\right)^2=\left(x^2-y^2\right)^2=x^4-2x^2y^2+y^4\)
Đúng 2
Bình luận (0)
Ta có: (x2+2xy+y2)(x2-2xy+y2)
= (x+y)2(x-y)2=[(x+y)(x-y)]2
= (x2-y2)2=x4-2x2y2+y4
Đúng 1
Bình luận (0)