a) S = 42; P = 441  ⇒   S 2   –   4 P   =   42 2   –   4 . 441   =   0

⇒ u và v là hai nghiệm của phương trình:  x 2   –   42 x   +   441   =   0

Có:   Δ ’   =   ( - 21 ) 2   –   441   =   0

⇒ Phương trình có nghiệm kép  x 1   =   x 2   =   - b ’ / a   =   21 .

Vậy u = v = 21.

b) S = -42; P = -400  ⇒   S 2   –   4 P   =   ( - 42 ) 2   –   4 . ( - 400 )   =   3364   >   0

⇒ u và v là hai nghiệm của phương trình:  x 2   +   42 x   –   400   =   0

Có  Δ ’   =   21 2   –   1 . ( - 400 )   =   841

⇒ Phương trình có hai nghiệm phân biệt:

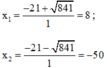
Vậy u = 8; v = -50 hoặc u = -50; v = 8.

c) u – v = 5 ⇒ u + (-v) = 5

u.v = 24 ⇒ u.(-v) = -uv = -24.

Ta tìm u và –v. Từ đó, ta dễ dàng tính được u và v.

S= u + (-v) = 5; P = u. (-v) = -24 ⇒  S 2   –   4 P   =   5 2   –   4 . ( - 24 )   =   121   >   0

⇒ u và –v là hai nghiệm của phương trình:  x 2   –   5 x   –   24   =   0

Có  Δ   =   ( - 5 ) 2   –   4 . 1 . ( - 24 )   =   121

⇒ Phương trình có hai nghiệm phân biệt

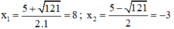
⇒ u = 8; -v = -3 hoặc u = -3; -v = 8

⇒ u = 8; v = 3 hoặc u = -3; v = -8.

a)   S   =   32 ;   P   =   231   ⇒   S 2   –   4 P   =   322   –   4 . 231   =   100   >   0

⇒ Tồn tại u và v là hai nghiệm của phương trình:  x 2   –   32 x   +   231   =   0 .

Ta có:  Δ   =   ( - 32 ) 2   –   4 . 231   =   100   >   0

⇒ PT có hai nghiệm:

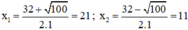
Vậy u = 21 ; v = 11 hoặc u = 11 ; v = 21.

b) S = -8; P = -105  ⇒   S 2   –   4 P   =   ( - 8 ) 2   –   4 . ( - 105 )   =   484   >   0

⇒ u và v là hai nghiệm của phương trình:  x 2   +   8 x   –   105   =   0

Ta có:  Δ ’   =   4 2   –   1 . ( - 105 )   =   121   >   0

Phương trình có hai nghiệm:

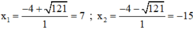
Vậy u = 7 ; v = -15 hoặc u = -15 ; v = 7.

c) S = 2 ; P = 9 ⇒  S 2   –   4 P   =   2 2   –   4 . 9   =   - 32   <   0

⇒ Không tồn tại u và v thỏa mãn.

a) S = 12, P = 28  ⇒   S 2   –   4 P   =   32   >   0

⇒ u, v là hai nghiệm của phương trình:  x 2   –   12 x   +   28   =   0 .

Có a = 1; b = -12; c = 28   ⇒   Δ ’   =   ( - 6 ) 2   –   28   =   8   >   0

Phương trình có hai nghiệm  x 1   =   6   +   2 √ 2 ;   x 2   =   6   -   2 √ 2

Vì u > v nên u = 6 + 2√2 và v = 6 - 2√2

b) S = 3; P = 6  ⇒   S 2   –   4 P   =   - 15   <   0

Vậy không tồn tại u, v thỏa mãn yêu cầu.

\(u+v=1\Rightarrow v=1-u\)

Thế vào \(uv=-42\Rightarrow u\left(1-u\right)=-42\)

\(\Rightarrow u^2-u-42=0\Rightarrow\left[{}\begin{matrix}u=7\Rightarrow v=-6\\u=-6\Rightarrow v=7>u\left(loại\right)\end{matrix}\right.\)

a) u + v = 42, uv = 441 => u, v là nghiệm của phương trình:

x² – 42x + 441 = 0

∆’ = 21² – 441 = 441 – 441 = 0, √∆’ = 0; x₁ = x₂ = 21

Vậy u = v = 21

b) u + v = -42, uv = -400, u, v là nghiệm của phương trình:

x² + 42x – 400 = 0

∆’ = 441 + 400 = 841, √∆’ = 29; x₁ = 8, x₂ = -50. Do đó:

u = 8, v = -50 hoặc u = -50, v = 8

c) u – v = 5, uv = 24. Đặt –v = t, ta có u + t = 5, ut = -24, ta tìm được:

u = 8, t = -3 hoặc u = -3, t = 8. Do đó:

u = 8, v = 3 hoặc u = -3, t = 8.

a) u + v = 42, uv = 441 => u, v là nghiệm của phương trình:

x2 – 42x + 441 = 0

∆’ = 212 – 441 = 441 – 441 = 0, √∆’ = 0; x1 = x2 = 21

Vậy u = v = 21

b) u + v = -42, uv = -400, u, v là nghiệm của phương trình:

x2 + 42x – 400 = 0

∆’ = 441 + 400 = 841, √∆’ = 29; x1 = 8, x2 = -50. Do đó:

u = 8, v = -50 hoặc u = -50, v = 8

c) u – v = 5, uv = 24. Đặt –v = t, ta có u + t = 5, ut = -24, ta tìm được:

u = 8, t = -3 hoặc u = -3, t = 8. Do đó:

u = 8, v = 3 hoặc u = -3, t = 8.

S = 12, P = 28 ⇒ S2 – 4P = 32 > 0

⇒ u, v là hai nghiệm của phương trình: x2 – 12x + 28 = 0.

Có a = 1; b = -12; c = 28 ⇒ Δ’ = (-6)2 – 28 = 8 > 0

Phương trình có hai nghiệm x1 = 6 + 2√2; x2 = 6 - 2√2

Vì u > v nên u = 6 + 2√2 và v = 6 - 2√2

Ta có S = u + v = 15, P = uv = 36. Nhận thấy S 2 = 225 > 144 = 4P nên u, v là hai nghiệm của phương trình

x 2 – 15x + 36 = 0 ⇔ (x – 12)(x – 3) = 0  ⇔ x = 12 x = 3

Vậy u = 12; v = 3 (vì u > v) nên u – v = 12 – 3 = 9

Đáp án: C

a) u và v là nghiệm của phương trình: x² – 32x + 231 = 0

∆’ = 16² – 231 = 256 – 231 = 25, \(\sqrt{\text{∆}'}\) = 5 . x₁ = 21, x₂ = 11

Vậy u = 21, v = 11 hoặc u = 11, v = 21

b) u, v là nghiệm của phương trình:

x² + 8x – 105 = 0, ∆’ = 16 + 105 = 121, \(\sqrt{\text{∆}'}\) = 11 . x = -4 + 11 = 7

x₂ = -4 – 11 = -15

Vậy u = 7, v = -15 hoặc u = -15, v = 7

c) Vì 2² – 4 . 9 < 0 nên không có giá trị nào của u và v thỏa mãn điều kiện đã cho.

a) u và v là nghiệm của phương trình: x2 – 32x + 231 = 0

∆’ = 162 – 231 = 256 – 231 = 25, √∆' = 5 . x1 = 21, x2 = 11

Vậy u = 21, v = 11 hoặc u = 11, v = 21

b) u, v là nghiệm của phương trình:

x2 + 8x – 105 = 0, ∆’ = 16 + 105 = 121, √∆' = 11 . x = -4 + 11 = 7

x2 = -4 – 11 = -15

Vậy u = 7, v = -15 hoặc u = -15, v = 7

c) Vì 22 – 4 . 9 < 0 nên không có giá trị nào của u và v thỏa mãn điều kiện đã cho.

\(\Rightarrow\)U, V là ng₀ của pt:

a) \(X^2-15X+36=0\)

\(\Rightarrow\left[{}\begin{matrix}X=12\\X=3\end{matrix}\right.\)

Vậy (U;V)=(12;3);(3;12).

b) \(X^2-4X+7=0\left(vng_0\right)\)

Vậy không tìm được U và V.

c) \(X^2+12X+20=0\)

\(\Rightarrow\left\{{}\begin{matrix}X=-2\\X=-10\end{matrix}\right.\)

Vậy (U;V)=(-2;-10);(-10;-2).