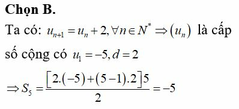cho day so Un duoc xac dinh boi U1=U2=1;U3=3,2Un+3=3Un+2+Un+1-5un.tinh U20,U30
Những câu hỏi liên quan
cho day so voi cac so hang tong quat duoc cho boi cong thuc;
Un=\(\frac{\left(13+\sqrt{3}\right)^n-\left(13-\sqrt{3}\right)n}{2\sqrt{3}}\) voi n=1,2,3,.........
tinh U1,U2,U3,U4,U5,U6,U7,U8,U9,U10
Lap cong thuc truy hoi tinh Un+1 theo Un va Un-1
Lap quy trinh an phim lien tuc tinh Un+1 theo Un va Un-1
đề sai nhỉ, sửa: \(U_n=\frac{\left(13+\sqrt{3}\right)^n-\left(13-\sqrt{3}\right)^n}{2\sqrt{3}}\)
a/ thay n = 1 => U1=1 (DÙNG CALC NHÉ)
n=2 => U2=26
n=3 => U3= 510
tương tự : U4 =8944; U5=147884; U6=2360280; U7=368185536; U8=565475456; U9=8590484880; U10=129483681183,992
b/ công thức tổng quát có dạng Un+1 = aUn + bUn-1
n=2 => U3 = aU2 + bU1 => 510 = 26a + b
n=3 => u4 = aU3 + bU2 => 8944 = 510a + 26b
giải HPT => a = 26; b= -166
vậy công thức là: Un+1 = 26Un - 166Un-1
Đúng 0
Bình luận (0)
Cau 3 : xac dinh 5 so hang dau cua day so
(Un) biet Un = 2n - 1
U1 = 2.1 - 1 = 1
U2 = 2.2 - 1 = 3
U3 = 2.3 - 1 = 5
U4 = 2.4 - 1 = 7
U5 = 2.5 - 1 = 9
Đúng 0
Bình luận (0)
Cho n duong thangsao cho khong co ba duong thang nao dong quyva chung doi mot cat nhau . Xac dinh so mien duoc chia boi n duong thang tren
Giải mục 1 trang 59, 60, 61, 62 SGK Toán 11 tập 1 - Cánh Diều
13 tháng 7 2023 lúc 22:59
Cho cấp số nhân (un), với u1=1 và công bội q=\(\dfrac{1}{2}\).
a) So sánh |q| với 1.
b) Tính Sn=u1+u2+...+un.. Từ đó, hãy tính limSn.
a: |q|=1/2<1
b: Sn=U1+u2+...+un
\(S_n=\dfrac{1\left(1-\left(\dfrac{1}{2}\right)^n\right)}{1-\dfrac{1}{2}}=2\left(1-\left(\dfrac{1}{2}\right)^n\right)\)
=>\(lim\left(S_n\right)=2\)
Đúng 0
Bình luận (0)
bai1 : cho day so Un=\(\frac{\left(5+\sqrt{7}\right)^n-\left(5-\sqrt{7}\right)^n}{2\sqrt{7}}\)voi n=0,1,2,3
a, tinh 5 so hang dau tien U0,U1,U2,U3,U4
b, CMR: Un+2=10Un+1-18Un
c, Lap quy trinh bam phim lien tuc tinh Un+2 theo Un+1 va Un
Cho cấp số nhân
u
1
,
u
2
,
u
3
,
..
u
n
với công bội
q
q
≠
0
,
q
≠
1
.
Đặt
S
n
u...
Đọc tiếp
Cho cấp số nhân u 1 , u 2 , u 3 , .. u n với công bội q q ≠ 0 , q ≠ 1 . Đặt S n = u 1 + u 2 + u 3 + .. + u n . Khi đó ta có:
A. S n = u 1 q n − 1 q − 1
B. S n = u 1 q n − 1 − 1 q − 1
C. S n = u 1 q n + 1 q + 1
D. S n = u 1 q n − 1 − 1 q + 1
Chọn A.
Phương pháp:
Sử dụng công thức tính tổng của n số hạng đầu của cấp số nhân có số hạng đầu tiên là
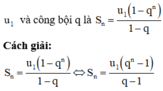
Đúng 0
Bình luận (0)
Cho dãy số
(
u
n
)
có
u
1
-
5
,
u
n
+
1
u
n...
Đọc tiếp
Cho dãy số ( u n ) có u 1 = - 5 , u n + 1 = u n + 2 , n ∈ N * . Tổng S 5 = = u 1 + u 2 + . . . + u 5 bằng
A. 5
B. – 5
C. – 15
D. – 24
Chọn B.
Phương pháp:
Công thức tính tổng n số hạng đầu tiên của cấp số cộng có số hạng đầu u1 và công sai d
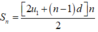
Cách giải:
Ta có: u n + 1 = u n + 2 , ∀ n ∈ ℕ *
⇒ ( u n ) là cấp số cộng có u 1 = - 5 , d = 2
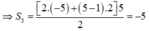
Đúng 0
Bình luận (0)
Cho dãy số
u
n
có
u
1
-
5
,
u
n
+
1
u
n
+
2
,
n
∈
N
*
.
Tổng
S
5
u
1...
Đọc tiếp
Cho dãy số u n có u 1 = - 5 , u n + 1 = u n + 2 , n ∈ N * . Tổng S 5 = u 1 + u 2 + . . . + u 5 bằng
A. 5
B. – 5
C. – 15
D. – 24
Cho cấp số nhân
u
1
,
u
2
,
u
3
,
.
.
u
n
với công bội
q
(
q
≠
0...
Đọc tiếp
Cho cấp số nhân u 1 , u 2 , u 3 , . . u n với công bội q ( q ≠ 0 , q ≠ 1 ) . Đặt S n = u 1 + u 2 + u 3 + . . . + u n . Khi đó ta có:
A. S n = u 1 ( q n - 1 ) q - 1
B. S n = u 1 ( q n - 1 - 1 ) q - 1
C. S n = u 1 ( q n + 1 ) q + 1
D. S n = u 1 ( q n - 1 - 1 ) q + 1
Chọn A
Phương pháp:
Sử dụng công thức tính tổng của n số hạng đầu của cấp số nhân có số hạng đầu tiên
là u 1 và công bội q là S n = u 1 ( 1 - q n ) 1 - q
Cách giải:
S n = u 1 ( 1 - q n ) 1 - q ⇔ S n = u 1 ( q n - 1 ) q - 1
Đúng 0
Bình luận (0)