Chọn A.
Phương pháp:
Sử dụng công thức tính tổng của n số hạng đầu của cấp số nhân có số hạng đầu tiên là
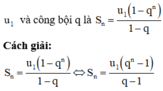
Chọn A.
Phương pháp:
Sử dụng công thức tính tổng của n số hạng đầu của cấp số nhân có số hạng đầu tiên là
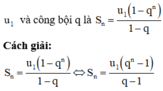
Bài 1: Cho A = ( 5m2 - 8m2 - 9m2) . ( -n3 + 4n3)
Với giá trị nào của m và n thì A ≥ 0
Bài 2: Cho S = 1 - 3 + 32 - 33 + ... + 398 - 399
a) Chứng minh S là bội của -20
b) Tính S, từ đó suy ra 3100 chia cho 4 dư 1
Bài 3: Tìm số nguyên n sao cho:
n - 1 là bội của n + 5 và n + 5 là bội của n - 1
Bài 4: Tìm số nguyên a, b biết (a,b) = 24 và a + b = -10
Toán lớp 6 nha, giải dùm mình, mình cảm ơn
Cho n số a1,a2,......,an biết rằng mỗi số trong chúng bằng 1 hoặc -1 và:
a1.a2+a2.a3+..........+an-1.an+an.a1=0
C/m n chia hết cho 4
Cho cấp số nhân ( u n ) có u n = 2 ( - 3 ) n + 1 . Tìm công bội q của cấp số nhân đó
A. q = 6 ( 3 + 1 )
B. q = - 6 ( 3 + 1 )
C. q = 3
D. q = - 3
Cho một cấp số nhân có n số hạng. Số hạng đầu tiên là 1, công bội là q và tổng là S. Trong đó q và S đều khác 0. Tổng các số hạng của cấp số nhân mới được thành bằng cách thay đổi mỗi số hạng của cấp số nhân ban đầu bằng nghịch đảo của nó là:
A. 1 S .
B. 1 q n . S .
C. S q n − 1 .
D. q n S .
Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 5 n − 1 , n = 1 , 2 , 3 ... Tìm số hạng đầu u 1 và công bội q của cấp số nhân đó.
A. u 1 = 5 , q = 6
B. u 1 = 4 , q = 5
C. u 1 = 5 , q = 4
D. u 1 = 6 , q = 5
Câu1: Cho số xyz chia hết cho 37. Chứng minh rằng số yzx chia hết cho 37
Câu2: có hay không 2 số tự nhiên x và y sao cho: 2002x + 5648y = 203 253 ?
Câu3: từ 1 đến 1000 có bao nhiêu số chia hết cho 2, có bao nhiêu số chia hết cho 5 ?
Câu4: tích ( n+2002 ).( n+2003 ) có chia hết cho 2 không? giải thích?
Câu5: tìm x,y để số 30xy chia hết cho cả 2 và 3, và chia cho 5 dư 2
Câu6: Viết số tự nhiên nhỏ nhất có 5 chữ số, tận cùng bằng 6 và chia hết cho 9.
Câu7:
a, Có bao nhiêu số có 2 chữ số chia hết cho 9 ?
b, Tìm tổng các số có 2 chữ số chia hết cho 9 .
Câu8: chứng minh rằng:
a, 102002 + 8 chia hết cho cả 9 và 2 .
b, 102004 + 14 chia hết cho cả 2 và 3 .
Câu9: tìm tập hợp A các số tự nhiên x là ước của 75 và là bội của 3.
Câu10: tìm các số tự nhiên x,y sao cho: ( 2x + 1 ). ( y - 5 ) = 12
Câu11: số ababab là số nguyên tố hay hợp số ?
Câu12: chứng minh rằng số abcabc chia hết ít nhất cho 3 số nguyên tố.
Câu13: chứng minh rằng: 2001 . 2002 . 2003 . 2004 + 1 là hợp số.
Câu14: tướng Trần Hưng Đạo đánh tan 50 vạn quân nguyên năm abcd, biết : a là số tự nhiên nhỏ nhất khác 0 ; b là số nguyên tố nhỏ nhất; c là hợp số chẵn lớn nhất có một chữ số; d là số tự nhiên liền sau số nguyên tố lẻ nhỏ nhất. Vậy abcd là năm nào ?
Câu15: cho p là một số nguyên tố lớn hơn 3 và 2p + 1 cũng là một số nguyên tố, thì 4p + 1 là số nguyên tố hay hợp số ? vì sao ?
Câu16: tìm 3 số tự nhiên liên tiếp có tích bằng 19 656.
Câu17: tìm số tụ nhiên n biết rằng: 1 + 2 + 3 +...+ n = 1275
Câu18: tìm số chia và thương của một phép chia, biết số bị chia là 150 và số dư là 7.
Câu19: tìm giao của 2 tập hợp A và B :
a, A là tập hợp các số tự nhiên chia hết cho 3. B là tập hợp các số tự nhiên chia hết cho 9.
b, A là tập hợp các số nguyên tố. B là tâp hợp các hợp số.
c, A là tập hợp các số nguyên tố bé hơn 10. B là tập hợp các chữ số lẻ.
--------- Hết---------
GIÚP VỚI, MAI NỘP RỒI.
Cho u n là cấp số cộng có công sai là d, v n là cấp số nhân có công bội là q và các khẳng định
I ) u n = d + u n − 1 ∀ n ≥ 2, n ∈ N
I I ) v n = q n v 1 ∀ n ≥ 2, n ∈ N
I I I ) u n = u n − 1 + u n + 1 2 ∀ n ≥ 2, n ∈ N
I V ) v n − 1 v n = v n − 1 2 ∀ ≥ 2, n ∈ N
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
A. 4
B. 2
C. 3
D. 5
Cho cấp số nhân u n có u 1 = 3 công bội q= -2 biết u n = 192 . Tìm n?
A. n = 7
B. n = 5
C. n = 6
D. n = 8
Cho dãy u(n) thỏa mãn log 3 u 1 2 - 3 log u 5 = log 3 u 2 + 9 - log u 1 6 và u n + 1 = u n + 3 u 1 > 0 với mọi n≥1 Đặt S n = u 1 + u 2 + . . . + u n Tìm giá trị nhỏ nhất của n để S n > 5 n 2 + 2018 2
A. 1647
B. 1650
C. 1648
D. 1165